(本题满分16分,第(1)小题6分,第(2)小题10分)
已知圆 ,点
,点 ,点
,点 在圆
在圆 上运动,
上运动, 的垂直平分线交
的垂直平分线交 于点
于点 .
.
(1)求动点 的轨迹
的轨迹 方程;
方程;
(2)过点 且斜率为
且斜率为 的动直线
的动直线 交曲线
交曲线 于
于 两点,在
两点,在 轴上是否存在定点
轴上是否存在定点 ,使以
,使以 为直径的圆恒过这个点?若存在,请求出点
为直径的圆恒过这个点?若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
已知函数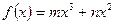 (
( )在
)在 时有极值,其图象在点
时有极值,其图象在点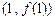 处的切线与直线
处的切线与直线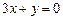 平行。
平行。
(1)求m,n的值; (2)求函数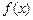 的单调区间。
的单调区间。
某工厂有A、B两种配件生产甲、乙两种产品,每生产一件甲产品使用4个A配件耗时1h,每生产一件乙产品使用4个B配件耗时2h,该厂每天最多可从配件厂获得16个A配件和12个B配件,按每天8h计算,若生产一件甲产品获利2万元,生产一件乙产品获利3万元,采用哪种生产安排利润最大?
在△ABC中,已知B=45°,D是BC边上的一点,AB=5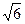 ,AC="14," DC=6,求AD的长.
,AC="14," DC=6,求AD的长.
已知函数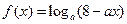
(1)若 ,求实数
,求实数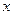 的取值范围;
的取值范围;
(2)若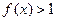 在区间[1,2]上恒成立,求实数
在区间[1,2]上恒成立,求实数 的取值范围.
的取值范围.
若数列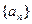 的前
的前 项和为
项和为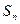 ,点
,点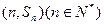 均在函数
均在函数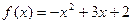 的图象上
的图象上
(1)求数列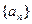 的通项公式;
的通项公式;
(2)若数列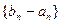 是首项为1,公比为
是首项为1,公比为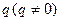 的等比数列,求数列
的等比数列,求数列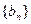 的前
的前 项和
项和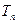 .
.