在平面直角坐标系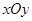 中,抛物线
中,抛物线 过点
过点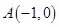 ,
,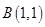 ,与
,与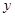 轴交于点
轴交于点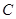 .
.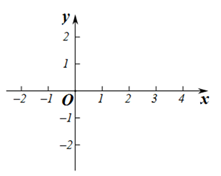
(1)求抛物线 的函数表达式;
的函数表达式;
(2)若点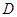 在抛物线
在抛物线 的对称轴上,当
的对称轴上,当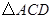 的周长最小时,求点
的周长最小时,求点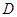 的坐标;
的坐标;
(3)在抛物线 的对称轴上是否存在点
的对称轴上是否存在点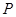 ,使
,使 成为以
成为以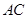 为直角边的直角三角形?若存在,求出点
为直角边的直角三角形?若存在,求出点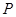 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(本题7分)如图,点B、F、C、E在一条直线上,FB=CE,AC=DF,请从下列三个条件:①AB=DE;②∠A=∠D;③∠ACB=∠DFE中选择一个合适的条件,使AB∥ED成立,并给出证明.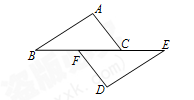
(1)选择的条件是(填序号)
(2)证明:
(本题7分)如图,在长度为1个单位长度的正方形网格中,点A、B、C在小正方形的顶点上.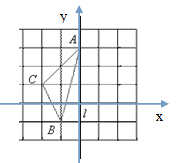
(1)在图中画出与△ABC关于直线l成轴对称的△A′B′C′;则点B′、 C′的坐标分别为(、) (、)
(2)在直线l上找一点P(在答题纸上图中标出),使PB+PC的长最短,这个最短长度的平方值是.
某校计划在暑假期间组织学生外出旅游,如果单独租用45座的客车若干辆,恰好坐满;如果单独租用60座的客车,可少租一辆,并且余30个座位。求外出旅游的学生人数是多少?单租45座客车需多少辆?
某公司6天内货品进出仓库的吨数如下:(“ ”表示进库 ,“—”表示出库+21,-32,-16,+35,-38,-20
”表示进库 ,“—”表示出库+21,-32,-16,+35,-38,-20
(1)经过这6天,仓库里的货品是(填“增多了”还是“减少了”).
(2)经过这6天,仓库管理员结算发现仓库里还有货品580吨,那么6天前仓库里有货品多少吨?
(3)如果进出的装卸费都是每吨4元,那么这6天要付多少元装卸费?
观察下列等式:
第1个等式:a1=  =
=  ×(1﹣
×(1﹣ );第2个等式:a2=
);第2个等式:a2=  =
=  ×(
×( ﹣
﹣ );
);
第3个等式:a3=  =
= ×(
×( ﹣
﹣ );第4个等式:a4=
);第4个等式:a4=  =
=  ×(
×( ﹣
﹣ );
);
…
请解答下列问题:
(1)按以上规律列出第5个等式:a5=——_=_________;
(2)用含有n的代数式表示第n个等式:an=_________=__________(n为正整数);
(3)求a1+a2+a3+a4+…+a100。