如图,AB是⊙O的直径,OD垂直于弦AC于点E,且交⊙O于点D,F是BA延长线上一点,若∠CDB=∠BFD.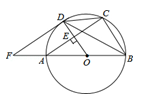
(1)求证:FD是⊙O的一条切线;
(2)若AB=10, AC=8,求DF的长.
(·辽宁本溪)如图1,在△ABC中,AB=AC,射线BP从BA所在位置开始绕点B顺时针旋转,旋转角为α(0°<α<180°)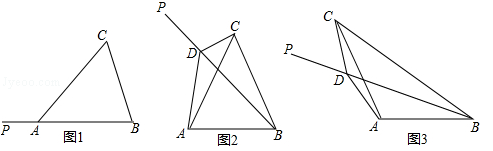
(1)当∠BAC=60°时,将BP旋转到图2位置,点D在射线BP上.若∠CDP=120°,则∠ACD ∠ABD(填“>”、“=”、“<”),线段BD、CD与AD之间的数量关系是 ;
(2)当∠BAC=120°时,将BP旋转到图3位置,点D在射线BP上,若∠CDP=60°,求证:BD﹣CD=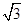 AD;
AD;
(3)将图3中的BP继续旋转,当30°<α<180°时,点D是直线BP上一点(点P不在线段BD上),若∠CDP=120°,请直接写出线段BD、CD与AD之间的数量关系(不必证明).
(·辽宁本溪)张老师利用休息时间组织学生测量山坡上一棵大树CD的高度,如图,山坡与水平面成30°角(即∠MAN=30°),在山坡底部A处测得大树顶端点C的仰角为45°,沿坡面前进20米,到达B处,又测得树顶端点C的仰角为60°(图中各点均在同一平面内),求这棵大树CD的高度(结果精确到0.1米,参考数据: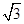 ≈1.732)
≈1.732)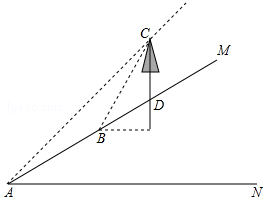
(·吉林长春)如图,在等边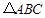 中,
中,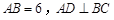 于点
于点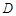 ,点
,点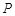 在边
在边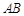 上运动,过点
上运动,过点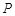 作
作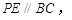 与边
与边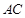 交于点
交于点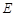 ,连结
,连结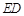 ,以
,以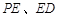 为邻边作□
为邻边作□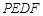 ,设□
,设□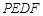 与
与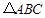 重叠部分图形的面积为
重叠部分图形的面积为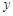 ,线段
,线段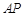 的长为
的长为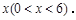
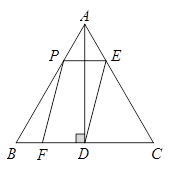
(1)求线段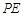 的长(用含
的长(用含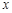 的代数式表示);
的代数式表示);
(2)当四边形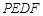 为菱形时,求
为菱形时,求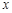 的值;
的值;
(3)求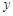 与
与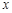 之间的函数关系式;
之间的函数关系式;
(4)设点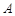 关于直线
关于直线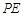 的对称点为点
的对称点为点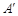 ,当线段
,当线段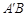 的垂直平分线与直线
的垂直平分线与直线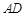 相交时,设其交点为
相交时,设其交点为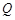 ,当点
,当点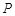 与点
与点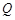 位于直线
位于直线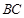 同侧(不包括点
同侧(不包括点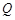 在直线
在直线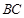 上)时,直接写出
上)时,直接写出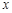 的取值范围.
的取值范围.
(·吉林长春)如图,海上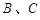 两岛分别位于
两岛分别位于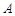 岛的正东和正北方向,一艘船从
岛的正东和正北方向,一艘船从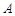 岛出发,以18海里/时的速度向正北方向航行2小时到达
岛出发,以18海里/时的速度向正北方向航行2小时到达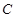 岛,此时测得
岛,此时测得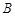 岛在
岛在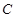 岛的南偏东
岛的南偏东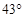 ,求
,求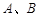 两岛之间的距离.(结果精确到0.1海里)
两岛之间的距离.(结果精确到0.1海里)
【参考数据: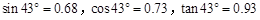 】
】
(·吉林省)如图,一艘海轮位于灯塔P的北偏东53°方向,距离灯塔100海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处.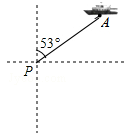
(1)在图中画出点B,并求出B处与灯塔P的距离(结果取整数);
(2)用方向和距离描述灯塔P相对于B处的位置.
(参考数据:sin53°=0.80,cos53°=0.60,tan53°=0.33,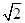 =1.41)
=1.41)