(本题10分)
(1)计算: 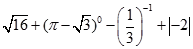 .
.
(2)解方程: .
.
在△ABC中,AB=AC,BD=CD,CE⊥AB于E,求证:△ABD∽△CBEA
解方程:
(1)(x+8)(x+1)=-12
(2)x(5x+4)=5x+4
如图,抛物线 与
与 轴交于A (-1,0),B (5,0)两点,直线
轴交于A (-1,0),B (5,0)两点,直线 与y轴交于点
与y轴交于点 ,与
,与 轴交于点
轴交于点 .点
.点 是x轴上方的抛物线上一动点,过点
是x轴上方的抛物线上一动点,过点 作
作 ⊥
⊥ 轴于点
轴于点 ,交直线
,交直线 于点
于点 .设点
.设点 的横坐标为
的横坐标为 .
.
(1)求抛物线的解析式;
(2)若 ,求
,求 的值;
的值;
(3)若点 是点
是点 关于直线
关于直线 的对称点,是否存在点
的对称点,是否存在点 ,使点
,使点 落在
落在 轴上?若存在,请直接写出相应的点
轴上?若存在,请直接写出相应的点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)
如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,点B是⊙O上一点,连接BP并延长,交直线l于点C,使得AB=AC.
(1)求证:AB是⊙O的切线;
(2)若PC=2 ,OA=3,求⊙O的半径.
,OA=3,求⊙O的半径.