如图，已知抛物线
的焦点在抛物线
上．
（Ⅰ）求抛物线
的方程及其准线方程；
（Ⅱ）过抛物线上的动点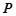
作抛物线
的两条切线
、
， 切点为
、
．若、的斜率乘积为
，且
，求
的取值范围．
（本小题满分8分） 设
（1）求函数f(x)的单调区间.（2）求极值点与极值.
（本小题满分8分）求椭圆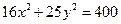
的长轴和短轴的长、离心率、焦点的坐标.
（本小题满分10分）如图，椭圆C: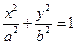
的焦距为
2，离心率为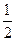
。
（1）求椭圆C的方程
（2）设
是过原点的直线，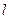
是与垂直相交于P点且与椭圆相交于A、B两点的直线，
，是否存在上述直线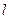使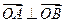
成立？若存在，求出直线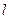的方程；若不存在，请说明理由。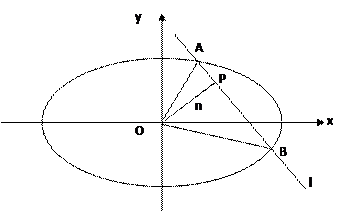
（本小题满分10分）如图，四棱锥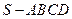
的底面是正方形，每条侧棱长都是底面边长的
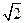倍，P为侧棱SD上的点。
（1）若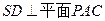
,求二面角
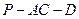的大小；
（2）在侧棱SC上是否存在一点E，使得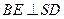
，若存在，求
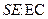的值；若不存在，试说明理由。
（本小题满分8分）设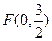
，动圆P经过点F且和直线
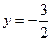相切，记动圆的圆心P的轨迹为曲线W.
(1)求曲线W的方程；
（2）过点F作互相垂直的直线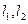
分别交曲线W与A、B和C、D，求四边形ACBD面积的最小值。