设椭圆 的方程为 ,点 为坐标原点,点 的坐标为 ,点 的坐标为 ,点 在线段 上,满足 ,直线 的斜率为 .
(Ⅰ)求
的离心率
;
(Ⅱ)设点
的坐标为
,
为线段
的中点,证明:
.
(理)已知直三棱柱 中,
中,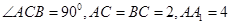 ,
,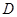 是棱
是棱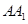 的中点.如图所示.
的中点.如图所示.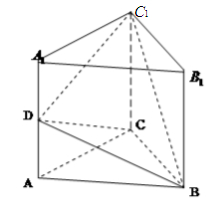
(1)求证: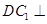 平面
平面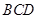 ;
;
(2)求二面角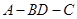 的大小.
的大小.
如下图所示,椭圆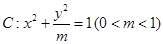 的左顶点为
的左顶点为 ,
,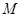 是椭圆
是椭圆 上异于点
上异于点 的任意一点,点
的任意一点,点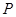 与点
与点 关于点
关于点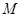 对称.
对称.
(1)若点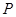 的坐标为
的坐标为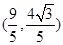 ,求
,求 的值;
的值;
(2)若椭圆 上存在点
上存在点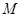 ,使得
,使得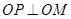 ,求
,求 的取值范围.
的取值范围.
已知函数
 .
.
(1)求函数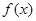 的单调区间和极值;
的单调区间和极值;
(2)若 对
对 上恒成立,求实数
上恒成立,求实数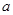 的取值范围.
的取值范围.
已知关于x的一元二次函数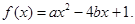
(1)设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为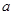 和
和 ,
,
求函数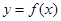 在区间[
在区间[ 上是增函数的概率;
上是增函数的概率;
(2)设点(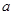 ,
, )是区域
)是区域 内的随机点,求函数
内的随机点,求函数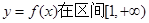 上是增函数的概率.
上是增函数的概率.
在直三棱柱ABC-A1B1C1中,已知AB=5,AC=4,BC=3,AA1=4,点D在棱AB上.
(1)求证:AC⊥B1C;
(2)若D是AB中点,求证:AC1∥平面B1CD.