某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为,求的分布列和数学期望.
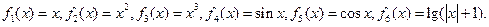 分别写在六张卡片上,放在一盒子中。 (1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数卡片则停止抽取,否则继续进行,求抽取次数
分别写在六张卡片上,放在一盒子中。 (1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数卡片则停止抽取,否则继续进行,求抽取次数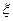 的分布列和数学期望.
的分布列和数学期望.
已知函数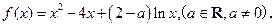
(1)当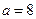 时,求函数
时,求函数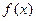 的单调区间;
的单调区间;
(2)求函数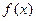 在区间
在区间 上的最小值.
上的最小值.
已知椭圆 的中心在原点,焦点在
的中心在原点,焦点在 轴上,椭圆上的点到焦点的距离的最小值为
轴上,椭圆上的点到焦点的距离的最小值为 ,离心率为
,离心率为 .
.
(1)求椭圆 的方程;
的方程;
(2)过点 作直线
作直线 交
交 于
于 、
、 两点,试问:在
两点,试问:在 轴上是否存在一个定点
轴上是否存在一个定点 ,使
,使 为定值?若存在,求出这个定点
为定值?若存在,求出这个定点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
已知直角梯形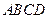 中,
中, ,
,
 过
过 作
作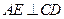 ,垂足为
,垂足为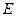 ,
,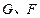 分别为
分别为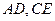 的中点,现将
的中点,现将 沿
沿 折叠使二面角
折叠使二面角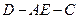 的平面角的正切值为
的平面角的正切值为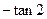 .
.
(1)求证: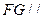 平面
平面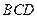 ;
;
(2)求异面直线 与
与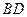 所成的角的余弦值;
所成的角的余弦值;
(3)求二面角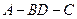 的大小.
的大小.
已知函数 ,数列
,数列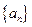 满足
满足 ,
,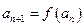 ,
, .
.
(1)求证: ;
;
(2)求证: 是递减数列;
是递减数列;
(3)设 的前
的前 项和为
项和为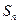 ,
,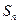 与
与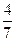 是否有确定的大小关系,如果有给出证明,如果没有给出反例.
是否有确定的大小关系,如果有给出证明,如果没有给出反例.