设数列
的前
项和为
.已知
.
(Ⅰ)求
的通项公式;
(Ⅱ)若数列
满足
,求
的前
项和
.
已知等差数列 中,
中, 
①求数列 的通项公式;
的通项公式;
②若数列 前
前 项和
项和 ,求
,求 的值。
的值。
设直线 是曲线
是曲线
 的一条切线,
的一条切线, .
.
(Ⅰ)求切点坐标及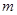 的值;
的值;
(Ⅱ)当 时,存在
时,存在
 ,求实数
,求实数 的取值范围.
的取值范围.
已知某公司生产某品牌服装的年固定成本为10万元,每生产千件需另投入2.7万元,设该公司年内共生产该品牌服装千件并全部销售完,每千件的销售收入为 万元,且
万元,且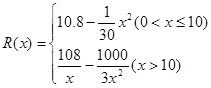 .
.
(1)写出年利润 (万元)关于年产品(千件)的函数解析式;
(万元)关于年产品(千件)的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获年利润最大?
(注:年利润=年销售收入-年总成本)
已知命题p:“ ”;命题q:“
”;命题q:“ ”.若命题“
”.若命题“ ”是真命题,求实数a的取值范围.
”是真命题,求实数a的取值范围.
已知函数f(x)=x2+2ax+3,x∈[-4,6].
(1)当a=-2时,求f(x)的最值;
(2)求实数a的取值范围,使y=f(x)在区间[-4,6]上是单调函数;