若
是一个三位正整数,且
的个位数字大于十位数字,十位数字大于百位数字,则称
为"三位递增数"(如137,359,567等).在某次数学趣味活动中,每位参加者需从所有的"三位递增数"中随机抽取1个数,且只能抽取一次.得分规则如下:若抽取的"三位递增数"的三个数字之积不能被5整除,参加者得0分;若能被5整除,但不能被10整除,得-1分;若能被10整除,得1分.
(Ⅰ)写出所有个位数字是5的"三位递增数" ;
(Ⅱ)若甲参加活动,求甲得分
的分布列和数学期望
.
某市芙蓉社区为了解家庭月均用水量(单位:吨),从社区中随机抽查100户,获得每户2013年3月的用水量,并制作了频率分布表和频率分布直方图(如图).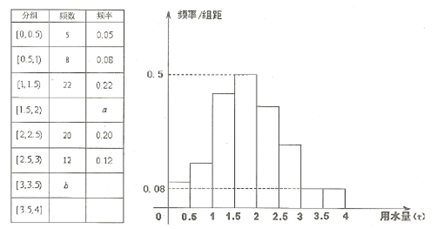
(Ⅰ)分别求出频率分布表中a、b的值,并估计社区内家庭月用水量不超过3吨的频率;
(Ⅱ)设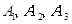 是月用水量为[0,2)的家庭代表.
是月用水量为[0,2)的家庭代表.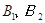 是月用水量为[2,4]的家庭代表.若从这五位代表中任选两人参加水价听证会,请列举出所有不同的选法,并求家庭代表
是月用水量为[2,4]的家庭代表.若从这五位代表中任选两人参加水价听证会,请列举出所有不同的选法,并求家庭代表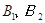 至少有一人被选中的概率.
至少有一人被选中的概率.
在如图所示的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.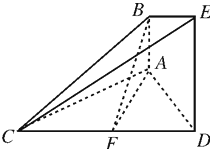
(Ⅰ)求证:AF∥平面BCE;
(Ⅱ)求证:平面BCE⊥平面CDE.
在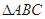 中,边
中,边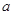 、
、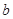 、
、 分别是角
分别是角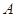 、
、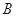 、
、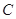 的对边,且满足
的对边,且满足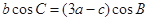 .
.
(Ⅰ)求 ;
;
(Ⅱ)若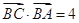 ,
,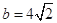 ,求边
,求边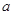 ,
, 的值.
的值.
已知圆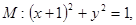 圆
圆 动圆
动圆 与圆
与圆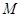 外切并与圆
外切并与圆 内切,圆心
内切,圆心 的轨迹为曲线
的轨迹为曲线 .
.
(1)求 的方程;
的方程;
(2)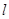 是与圆
是与圆 ,圆
,圆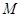 都相切的一条直线,
都相切的一条直线,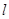 与曲线
与曲线 交于
交于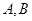 两点,当圆
两点,当圆 的半径最长时,求
的半径最长时,求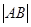 .
.
设等差数列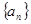 的前
的前 项和为
项和为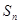 ,且
,且 ,
,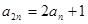 .
.
(1)求数列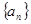 的通项公式;
的通项公式;
(2)设数列 满足
满足 ,求
,求 的通项公式;
的通项公式;
(3)求数列 前
前 项和
项和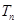 .
.