平面直角坐标系中,已知椭圆的离心率为,左、右焦点分别是,以为圆心以3为半径的圆与以为圆心以1为半径的圆相交,且交点在椭圆上.
(Ⅰ)求椭圆的方程;
(Ⅱ)设椭圆,为椭圆上任意一点,过点的直线交椭圆于两点,射线交椭圆于点.
(i)求的值;
(Ⅱ)求面积的最大值.
已知直线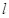 经过直线
经过直线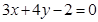 与直线
与直线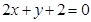 的交点
的交点 ,且垂直于直线
,且垂直于直线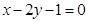 .
.
(Ⅰ)求直线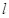 的方程;
的方程;
(Ⅱ)求直线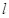 与两坐标轴围成的三角形的面积
与两坐标轴围成的三角形的面积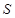
焦点在x轴上的双曲线过点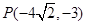 且点
且点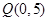 与两焦点的连线互相垂直。
与两焦点的连线互相垂直。
(1)求此双曲线的标准方程;
(2)过双曲线的右焦点倾斜角为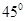 的直线与双曲线交于A、B两点,求
的直线与双曲线交于A、B两点,求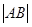 的长。
的长。
某高速公路某施工工地需调运建材100吨,可租用装载的卡车和农用车分别为10辆和20辆,若每辆卡车装载8吨,运费960元,每辆农用车装载2.5吨,运费360元,问两种车各租用多少辆时,才能一次性装完且总费用最低?
如图为函数y=Asin(ωx+φ)(A>0,ω>0)的图象的一部分,试求该函数的一个解析式.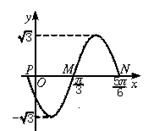
已知数列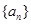 满足
满足 ,
,
(1)求 ;(2)判断20是不是这个数列的项,并说明理由; (3)求这个数列前n项的和
;(2)判断20是不是这个数列的项,并说明理由; (3)求这个数列前n项的和 。
。