设函数
,其中
.
(Ⅰ)讨论函数
极值点的个数,并说明理由;
(Ⅱ)若
成立,求
的取值范围.
(本小题满分12分)已知离心率为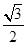 的椭圆
的椭圆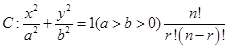 与直线
与直线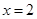 相交于
相交于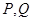 两点(点
两点(点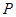 在
在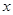 轴上方),且
轴上方),且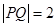 .点
.点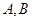 是椭圆上位于直线
是椭圆上位于直线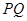 两侧的两个动点,且
两侧的两个动点,且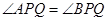 .
.
(Ⅰ)求椭圆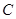 的标准方程;
的标准方程;
(Ⅱ)求四边形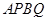 面积的取值范围.
面积的取值范围.
(本小题满分12分)小王在某社交网络的朋友圈中,向在线的甲、乙、丙随机发放红包,每次发放1个.
(Ⅰ)若小王发放5元的红包2个,求甲恰得1个的概率;
(Ⅱ)若小王发放3个红包,其中5元的2个,10元的1个.记乙所得红包的总钱数为X,求X的分布列和期望.
在如图所示的几何体中,四边形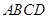 是等腰梯形,
是等腰梯形,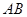 ∥
∥ ,
, ,
, .在梯形
.在梯形 中,
中,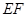 ∥
∥ ,且
,且 ,
,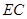 ⊥平面
⊥平面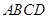 .
.
(Ⅰ)求证: ;
;
(Ⅱ)若二面角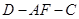 为
为 ,求
,求 的长.
的长.
(本小题满分12分) 已知函数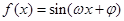 (
( ,
,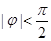 )图象的相邻两对称轴间的距离为
)图象的相邻两对称轴间的距离为 ,若将函数
,若将函数 的图象向左平移
的图象向左平移 个单位后图象关于
个单位后图象关于 轴对称.
轴对称.
(1)求使 成立的
成立的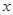 的取值范围;
的取值范围;
(2)设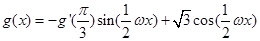 ,其中
,其中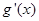 是
是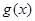 的导函数,若
的导函数,若 ,且
,且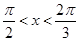 ,求
,求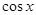 的值.
的值.
选修4—5:不等式选讲
设函数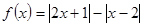
(1)求不等式 的解集;
的解集;
(2)若 恒成立,求实数
恒成立,求实数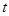 的取值范围.
的取值范围.