已知椭圆
,过原点的两条直线
和
分别于椭圆交于
、
和
、
,设
的面积为
.
(1)设
,
,用
、
的坐标表示点
到直线
的距离,并证明
;
(2)设
,
,
,求
的值;
(3)设
与
的斜率之积为
,求
的值,使得无论
与
如何变动,面积
保持不变.
定义:若各项为正实数的数列 满足
满足 ,则称数列
,则称数列 为“算术平方根递推数列”.
为“算术平方根递推数列”.
已知数列 满足
满足 且
且 点
点 在二次函数
在二次函数 的图像上.
的图像上.
(1)试判断数列
 是否为算术平方根递推数列?若是,请说明你的理由;
是否为算术平方根递推数列?若是,请说明你的理由;
(2)记
 ,求证:数列
,求证:数列 是等比数列,并求出通项公式
是等比数列,并求出通项公式 ;
;
(3)从数列 中依据某种顺序自左至右取出其中的项
中依据某种顺序自左至右取出其中的项 ,把这些项重新组成一个新数列
,把这些项重新组成一个新数列 :
: .若数列
.若数列 是首项为
是首项为 、公比为
、公比为 的无穷等比数列,且数列
的无穷等比数列,且数列 各项的和为
各项的和为 ,求正整数
,求正整数 的值.
的值.
已知函数 ,函数
,函数 是函数
是函数 的反函数.
的反函数.
(1)求函数 的解析式,并写出定义域
的解析式,并写出定义域 ;
;
(2)设 ,若函数
,若函数 在区间
在区间 内的图像是不间断的光滑曲线,求证:函数
内的图像是不间断的光滑曲线,求证:函数 在区间
在区间 内必有唯一的零点(假设为
内必有唯一的零点(假设为 ),且
),且 .
.
已知函数 .
.
(1)求函数 的单调递增区间;
的单调递增区间;
(2)在 中,内角
中,内角 所对边的长分别是
所对边的长分别是 ,若
,若 ,求
,求 的面积
的面积 的值.
的值.
在长方体 中,
中, ,
, 分别是所在棱
分别是所在棱 的中点,点
的中点,点 是棱
是棱 上的动点,联结
上的动点,联结 .如图所示.
.如图所示.
(1)求异面直线 所成角的大小(用反三角函数值表示);
所成角的大小(用反三角函数值表示);
(2)求以 为顶点的三棱锥的体积.
为顶点的三棱锥的体积.
设 满足约束条件
满足约束条件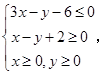 若目标函数
若目标函数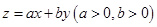 的最大值为10,则
的最大值为10,则 的最小值为
的最小值为