如图,椭圆
的离心率是
,过点
的动直线
与椭圆相交于
两点,当直线
平行与
轴时,直线
被椭圆
截得的线段长为
.

(1)求椭圆
的方程;
(2)在平面直角坐标系
中,是否存在与点
不同的定点
,使得
恒成立?若存在,求出点
的坐标;若不存在,请说明理由.
已知点A、B、C的坐标分别为A(3,0)、B(0,3)、C(cosα,sinα),
α∈(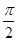 ,
, ).
).
(1)若|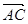 |=|
|=|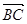 |,求角α的值;
|,求角α的值;
(2)若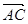 ·
·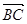 =-1,求
=-1,求 的值.
的值.
已知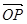 =
= ,
,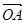 =
=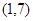 ,
,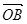 =
=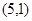 ,设
,设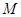 是直线
是直线 上一点,
上一点, 是坐标原点.
是坐标原点.
⑴求使 取最小值时的
取最小值时的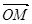 ; ⑵对(1)中的点
; ⑵对(1)中的点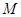 ,求
,求 的余弦值.
的余弦值.
已知函数y= cos2x+
cos2x+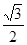 sinxcosx+1,x∈R.
sinxcosx+1,x∈R.
(1)求函数 的最小正周期;
的最小正周期;
(2)求函数 的单调减区间.
的单调减区间.
在数列 中,
中,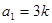 ,其中
,其中 ,对任意
,对任意 都有:
都有: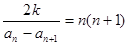 ;(1)求数列
;(1)求数列 的第2项和第3项;
的第2项和第3项;
(2)求数列 的通项公式
的通项公式 ,假设
,假设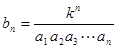 ,试求数列
,试求数列 的前
的前 项和
项和 ;
;
(3)若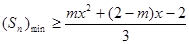 对一切
对一切 恒成立,求
恒成立,求 的取值范围。
的取值范围。
已知数列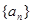 中,
中,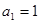 ,
,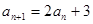 ,数列
,数列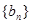 中,
中,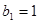 ,且点
,且点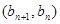 在直线
在直线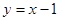 上。
上。
(1)求数列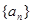 的通项公式;
的通项公式;
(2)求数列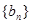 的前
的前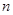 项和
项和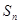 ;
;
(3)若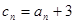 ,求数列
,求数列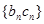 的前
的前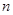 项和
项和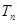 ;
;