已知函数
,其中
.
(Ⅰ)设
为
的导函数,讨论
的单调性;
(Ⅱ)证明:存在
,使得
恒成立,且
在区间
内有唯一解.
某商人将进货单价为8元的某种商品按10元一个销售时,每天可卖出100个,现在他采用提高售价,减少进货量的办法增加利润,已知这种商品销售单价每涨1元,销售量就减少10个.问他将每个商品售价定为多少元时,才能使每天的利润最大?
设全集U=R,集合A={x︱︱x-5︱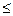 5},B={x︱x2+x
5},B={x︱x2+x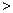 2},求A
2},求A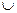 (
( uB).
uB).
在抛物线y=x2上求一点,使它到直线x-y-2=0的距离最短,并求此距离.
原点为顶点,坐标轴为对称轴,且焦点在直线x-2y-4=0上的抛物线方程为.
抛物线的顶点在原点,焦点是圆x2+y2-4x=0的圆心,斜率为2的直线l过焦点,且与抛物线、圆依次交于点A、B、C、D,则|AB|+|CD|的值等于______________.