选修4-4：坐标系与参数方程
在直角坐标系
中，直线
，圆
,以坐标原点为极点，
轴的正半轴为极轴建立极坐标系.
（Ⅰ）求
，
的极坐标方程；
（Ⅱ）若直线
的极坐标方程为
，设
与
的交点为
,
 ,求
的面积.
如图，椭圆的中心为原点O，离心率e=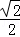
，一条准线的方程为x=2
．
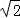（1）求该椭圆的标准方程．
（2）设动点P满足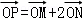
，其中M，N是椭圆上的点．直线OM与ON的斜率之积为﹣
．
问：是否存在两个定点F1，F2，使得|PF1|+|PF2|为定值．若存在，求F1，F2的坐标；若不存在，说明理由．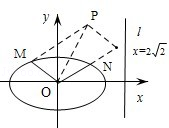
如图，在四面体ABCD中，平面ABC⊥ACD，AB⊥BC，AD=CD，∠CAD=30°
（1）若AD=2，AB=2BC，求四面体ABCD的体积．
（2）若二面角C﹣AB﹣D为60°，求异面直线AD与BC所成角的余弦值．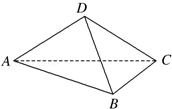
设f（x）=x3+ax2+bx+1的导数f′（x）满足f′（1）=2a，f′（2）=﹣b，其中常数a，b∈R．
（1）求曲线y=f（x）在点（1，f（1））处的切线方程．
（2）设g（x）=f′（x）e﹣x．求函数g（x）的极值．
某市公租房的房源位于A、B、C三个片区，设每位申请人只申请其中一个片区的房源，且申请其中任一个片区的房源是等可能的，求该市的任4位申请人中：
（1）恰有2人申请A片区房源的概率；
（2）申请的房源所在片区的个数的ξ分布列与期望．
设α∈R，f（x）=cosx（asinx﹣cosx）+cos2（
﹣x）满足
，求函数f（x）在
上的最大值和最小值．