设函数
.
(Ⅰ)讨论
的导函数
的零点的个数;
(Ⅱ)证明:当
时
.
(13)已知函数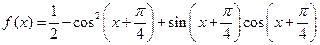
(I)求函数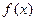 的最大值和周期;(II)设角
的最大值和周期;(II)设角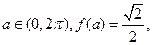 求
求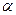 。
。
在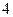 月份,有一新款服装投入某商场销售,
月份,有一新款服装投入某商场销售,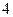 月
月 日该款服装仅销售出
日该款服装仅销售出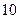 件,第二天售出
件,第二天售出 件,第三天销售
件,第三天销售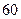 件,然后,每天售出的件数分别递增
件,然后,每天售出的件数分别递增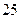 件,直到日销售量达到最大后,每天销售的件数分别递减
件,直到日销售量达到最大后,每天销售的件数分别递减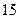 件,到月底该服装共销售出
件,到月底该服装共销售出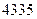 件.(Ⅰ)问
件.(Ⅰ)问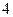 月几号该款服装销售件数最多?其最大值是多少?(Ⅱ)按规律,当该商场销售此服装超过
月几号该款服装销售件数最多?其最大值是多少?(Ⅱ)按规律,当该商场销售此服装超过 件时,社会上就流行,而日销售量连续下降,并低于
件时,社会上就流行,而日销售量连续下降,并低于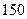 件时,则流行消失,问该款服装在社会上流行是否超过
件时,则流行消失,问该款服装在社会上流行是否超过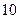 天?并说明理由。
天?并说明理由。
在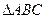 中,角
中,角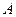 、
、 、
、 的对边分别为
的对边分别为 、
、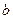 、
、 ,且
,且 ,
,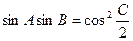 ,
, 边上中线
边上中线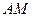 的长为
的长为 .
.
(Ⅰ) 求角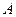 和角
和角 的大小;(Ⅱ) 求
的大小;(Ⅱ) 求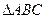 的面积.
的面积.
设数列 的前
的前 和为
和为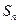 ,已知
,已知 ,
, ,
, ,
, ,
,
一般地, (
( ).
).
(Ⅰ)求 ;(Ⅱ)求
;(Ⅱ)求 ;(Ⅲ)求和:
;(Ⅲ)求和: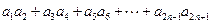 .
.
已知函数 (
( 为实常数).
为实常数).
(Ⅰ) 若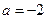 ,求证:函数
,求证:函数 在
在 上是增函数;
上是增函数;
(Ⅱ) 求函数 在
在 上的最小值及相应的
上的最小值及相应的 值;
值;
(Ⅲ) 若存在 ,使得
,使得
 成立,求实数
成立,求实数 的取值范围.
的取值范围.