(本题小满分12分)
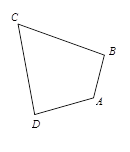
如图,平面四边形 中,角
中,角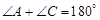 ,且
,且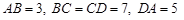 .
.
(Ⅰ)求∠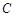 ;
;
(Ⅱ)求四边形 的面积
的面积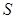 .
.
(本小题满分12分)
如图2,渔船甲位于岛屿 的南偏西
的南偏西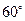 方向的
方向的 处,且与岛屿
处,且与岛屿 相距12海里,渔船乙以10海里/小时的速度从岛屿
相距12海里,渔船乙以10海里/小时的速度从岛屿 出发沿正北方向航行,若渔船甲同时从
出发沿正北方向航行,若渔船甲同时从 处出发沿北偏东
处出发沿北偏东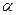 的方向追赶渔船乙,刚好用2小时追上.
的方向追赶渔船乙,刚好用2小时追上.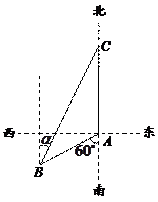
(1)求渔船甲的速度;
(2)求 的值.
的值.
如图,角 终边上一点P的坐标(3,4),将OP绕原点旋转
终边上一点P的坐标(3,4),将OP绕原点旋转 到
到 的位置,试求点
的位置,试求点 的坐标.
的坐标.
求函数 的定义域
的定义域
设函数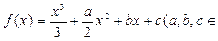 R),函数
R),函数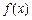 的导数记为
的导数记为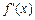 .
.
(1)若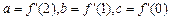 ,求a、b、c的值;
,求a、b、c的值;
(2)在(1)的条件下,记 ,求证:F(1)+ F(2)+ F(3)+…+ F(n)<
,求证:F(1)+ F(2)+ F(3)+…+ F(n)< N*);
N*);
(3)设关于x的方程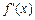 =0的两个实数根为α、β,且1<α<β<2.试问:是否存在正整数n0,使得
=0的两个实数根为α、β,且1<α<β<2.试问:是否存在正整数n0,使得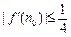 ?说明理由.
?说明理由.
已知动点 到定点
到定点 的距离与到定直线
的距离与到定直线 :
: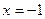 的距离相等,点C在直线
的距离相等,点C在直线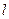 上。
上。
(1)求动点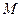 的轨迹方程。
的轨迹方程。
(2)设过定点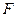 ,且法向量
,且法向量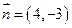 的直线与(1)中的轨迹相交于
的直线与(1)中的轨迹相交于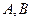 两点且点
两点且点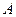 在
在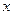 轴的上方。判断
轴的上方。判断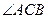 能否为钝角并说明理由。进一步研究
能否为钝角并说明理由。进一步研究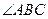 为钝角时点
为钝角时点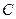 纵坐标的取值范围。
纵坐标的取值范围。