(本小题满分16分)
已知数列{an}的各项均为正数,其前n项的和为Sn,且对任意的m,n∈N*,
都有(Sm+n+S1)2=4a2ma2n.
(1)求的值;
(2)求证:{an}为等比数列;
(3)已知数列{cn},{dn}满足|cn|=|dn|=an,p(p≥3)是给定的正整数,数列{cn},{dn}的前p项的和分别为Tp,Rp,且Tp=Rp,求证:对任意正整数k(1≤k≤p),ck=dk.
在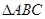 中,角
中,角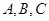 的对边分别为
的对边分别为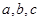 ,已知
,已知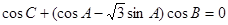 .
.
(Ⅰ)求角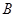 的大小;
的大小;
(Ⅱ)若 ,求△
,求△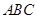 的面积.
的面积.
已知函数 ,若在定义域内存在
,若在定义域内存在 ,使得
,使得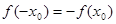 成立,则称
成立,则称 为函数
为函数 的局部对称点.
的局部对称点.
(1)若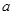 、
、 R且
R且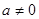 ,证明:函数
,证明:函数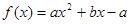 必有局部对称点;
必有局部对称点;
(2)若函数 在区间
在区间 内有局部对称点,求实数
内有局部对称点,求实数 的取值范围;
的取值范围;
(3)若函数 在R上有局部对称点,求实数
在R上有局部对称点,求实数 的取值范围.
的取值范围.
已知抛物线 (
( )的准线与
)的准线与 轴交于点
轴交于点 .
.
(1)求抛物线的方程,并写出焦点坐标;
(2)是否存在过焦点的直线 (直线与抛物线交于点
(直线与抛物线交于点 ,
, ),使得三角形
),使得三角形 的面积
的面积 ?若存在,请求出直线
?若存在,请求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
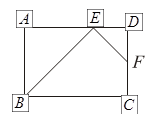
如图,在矩形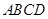 中,点
中,点 为边
为边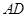 上的点,点
上的点,点 为边
为边 的中点,
的中点, 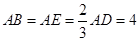 ,现将
,现将 沿
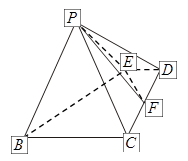
沿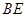 边折至
边折至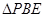 位置,且平面
位置,且平面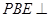 平面
平面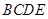 .
.
(Ⅰ)求证:平面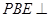 平面
平面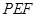 ;
;
(Ⅱ)求四棱锥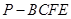 的体积.
的体积.
(本小题满分15分)已知△ABC中的三个内角A,B,C所对的边分别为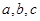 ,且满足
,且满足
(Ⅰ)求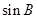 ;(Ⅱ)求△ABC的面积.
;(Ⅱ)求△ABC的面积.