为了分流地铁高峰的压力，某市发改委通过听众会，决定实施低峰优-优题课

已知函数 $f (x) = e^{x} - a (x + 2)$ .

（1）当 $a = 1$ 时，讨论 $f (x)$ 的单调性；

（2）若 $f (x)$ 有两个零点，求 $a$ 的取值范围.

如图， $D$ 为圆锥的顶点， $O$ 是圆锥底面的圆心， $△ ABC$ 是底面的内接正三角形， $P$ 为 $DO$ 上一点，∠ APC=90°．

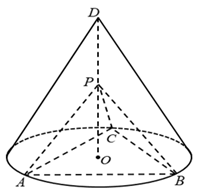
（1）证明：平面 PAB⊥平面 PAC；

（2）设 DO= $\sqrt{2}$ ，圆锥的侧面积为 $\sqrt{3} π$ ，求三棱锥 P− ABC的体积.

$△ ABC$ 的内角A，B，C的对边分别为a，b，c.已知B=150°.

（1）若a= $\sqrt{3}$ c，b=2 $\sqrt{7}$ ，求 $△ ABC$ 的面积；

（2）若sinA+ $\sqrt{3}$ sinC= $\frac{\sqrt{2}}{2}$ ，求C.

某厂接受了一项加工业务，加工出来的产品(单位：件)按标准分为 A ， B ， C ， D四个等级.加工业务约定：对于 A级品、 B级品、 C级品，厂家每件分别收取加工费90元，50元，20元；对于D级品，厂家每件要赔偿原料损失费50元.该厂有甲、乙两个分厂可承接加工业务.甲分厂加工成本费为25元/件，乙分厂加工成本费为20元/件.厂家为决定由哪个分厂承接加工业务，在两个分厂各试加工了100件这种产品，并统计了这些产品的等级，整理如下：

甲分厂产品等级的频数分布表

等级	A	B	C	D
频数	40	20	20	20

乙分厂产品等级的频数分布表

等级	A	B	C	D
频数	28	17	34	21

（1）分别估计甲、乙两分厂加工出来的一件产品为A级品的概率；

（2）分别求甲、乙两分厂加工出来的100件产品的平均利润，以平均利润为依据，厂家应选哪个分厂承接加工业务?

已知函数 $f (x) = |x - a^{2}| + | x - 2 a + 1 |$ .

（1）当 $a = 2$ 时，求不等式 $f (x) ⩾ 4$ 的解集；

（2）若 $f (x) ⩾ 4$ ，求 a的取值范围.

乘坐里程（单位：）
票价（单位：元）