已知抛物线
的焦点为
，抛物线上存在一点
到焦点的距离为
，且点在圆
上．
（Ⅰ）求抛物线
的方程；
（Ⅱ）已知椭圆
的一个焦点与抛物线的焦点重合，若椭圆
上存在关于直线
对称的两个不同的点，求椭圆的离心率
的取值范围．
对某校小学生进行心理障碍测试得到如下的列联表：
| 有心理障碍 |
没有心理障碍 |
总计 |
|
| 女生 |
10 |
30 |
|
| 男生 |
70 |
80 |
|
| 总计 |
20 |
110 |
将表格填写完整，试说明心理障碍与性别的关系？
附：
 |
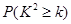0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3. 841 |
5.024 |
6.635 |
7.879 |
10.828 |
解关于
的不等式：
已知函数
．
（1）若不等式
的解集为
，求实数
的值；
（2）在（1）的条件下，若
对一切实数
恒成立，求实数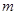
的取值范围。
设
，求证: 
已知函数
在
处取得极值.
（1）讨论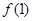
和
是函数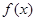
的极大值还是极小值；
（2）过点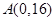
作曲线
的切线，求此切线方程.[