已知抛物线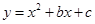 经过(0,-1),(3,2)两点.求它的解析式及顶点坐标.
经过(0,-1),(3,2)两点.求它的解析式及顶点坐标.
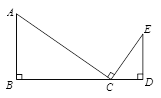
如图,在△ 和△
和△ 中,
中, ,
,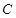 为线段
为线段 上一点,且
上一点,且 .
.
求证: .
.
解方程: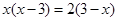 .
.
已知:用2辆A型车和1辆B型车载满货物一次可运货10吨;用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满货物.
根据以上信息,解答下列问题:
(1)1辆A型车和1辆车B型车都载满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱的租车方案,并求出最少租车费.
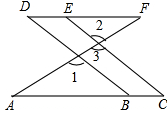
如图所示,点B、E分别在AC、DF上,BD、CE均与AF相交,∠1=∠2,∠C=∠D,求证:∠A=∠F.