如图①所示,在直角梯形ABCD中,∠BAD=90°,E是直线AB上一点,过E作直线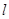 //BC,交直线CD于点F.将直线
//BC,交直线CD于点F.将直线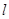 向右平移,设平移距离BE为
向右平移,设平移距离BE为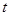 (t
(t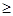 0),直角梯形ABCD被直线
0),直角梯形ABCD被直线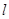 扫过的面积(图中阴影部份)为S,S关于
扫过的面积(图中阴影部份)为S,S关于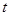 的函数图象如图②所示,OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
的函数图象如图②所示,OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.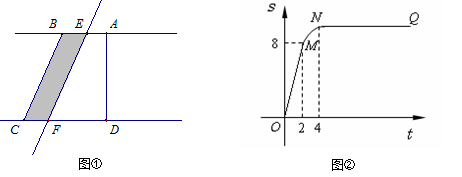
信息读取
(1)梯形上底的长AB= ;
(2)直角梯形ABCD的面积= ;
图象理解
(3)写出图②中射线NQ表示的实际意义;
(4)当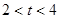 时,求S关于
时,求S关于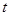 的函数关系式;
的函数关系式;
问题解决
(5)当t为何值时,直线l将直角梯形ABCD分成的两部分面积之比为1: 3.
宁波市政府为了了解本市市民对本届食品博览会的总体印象,利用最新引进的“计算机辅助电话访问系统”(简称CATI系统),采取电脑随机抽样的方式,对本市年龄在16—65岁之间的居民.进行了300个电话抽样调查.并根据每个年龄段的抽查人数和该年龄段对食博会总体印象感到满意的人数绘制了下图.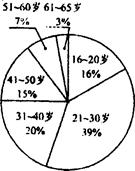
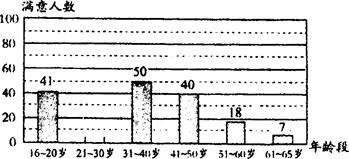
根据上图提供的信息回答下列问题:
(1)被抽查的居民中,人数最多的年龄段是岁;
(2)已知被抽查的300人中有82%的人对食博会总体印象感到满意,请你求出21~30岁年龄段的满意人数,并补全条形统计图;
(3)比较21~30岁和41~50岁这两个年龄段对食博会总体印象满意率的高低.
注:某年龄段的满意率=该年龄段满意人数÷该年龄段被抽查人数×l00%.
如图,AB是⊙O的直径,点C在⊙O上, AB=5,BC=3, 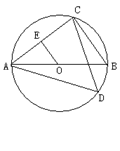
(1)若OE⊥AC于点E,求OE的长;
(2)若点D为优弧 上一点,求tan∠ADC的值.
上一点,求tan∠ADC的值.
在围棋盒中有x颗黑色棋子和y颗白色棋子,从盒中随机地取出一个棋子,如果它是黑色棋子的概率是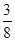 ,
,
(1)试写出y与x的函数关系式;(2)若往盒中再放进10颗黑色棋子,取得黑色棋子的概率为 ,求x和y的值.
,求x和y的值.
化简求值: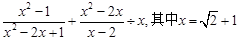 .
.
在平面直角坐标系中,二次函数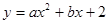 的图象与
的图象与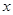 轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
轴交于A(-3,0),B(1,0)两点,与y轴交于点C.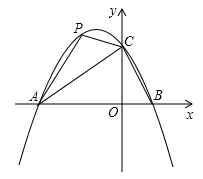
(1)求这个二次函数的解析式;
(2)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由;
(3)点Q是直线AC上方的抛物线上一动点,过点Q作QE垂直于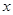 轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;
轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;