宁波市政府为了了解本市市民对本届食品博览会的总体印象,利用最新引进的“计算机辅助电话访问系统”(简称CATI系统),采取电脑随机抽样的方式,对本市年龄在16—65岁之间的居民.进行了300个电话抽样调查.并根据每个年龄段的抽查人数和该年龄段对食博会总体印象感到满意的人数绘制了下图.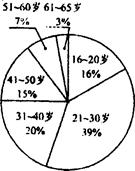
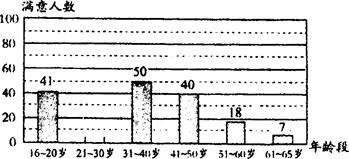
根据上图提供的信息回答下列问题:
(1)被抽查的居民中,人数最多的年龄段是 岁;
(2)已知被抽查的300人中有82%的人对食博会总体印象感到满意,请你求出21~30岁年龄段的满意人数,并补全条形统计图;
(3)比较21~30岁和41~50岁这两个年龄段对食博会总体印象满意率的高低.
注:某年龄段的满意率=该年龄段满意人数÷该年龄段被抽查人数×l00%.
已知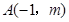 与
与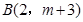 是反比例函数
是反比例函数 图象上的两个点。
图象上的两个点。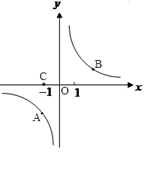
(1)求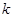 的值;
的值;
(2)求直线AB的函数解析式;
(3)若点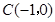 ,点
,点 是反比例函数
是反比例函数 图象上的一点,如果以
图象上的一点,如果以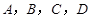 四点为顶点的四边形为梯形,请你求出点
四点为顶点的四边形为梯形,请你求出点 的坐标(能求出一个点即可)
的坐标(能求出一个点即可)
|
。
在 ABCD中,E、F分别是AB、CD的中点,连接AF、CE.
ABCD中,E、F分别是AB、CD的中点,连接AF、CE.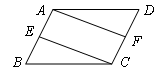
(1)求证:△BEC≌△DFA;
(2)连接AC,当CA=CB时,判断四边形AECF是什么特殊四边形?并证明你的结论.
为增强环保意识,某社区计划开展一次“减碳环保,减少用车时间”的宣传活动,对部分家庭五月份的平均每天用车时间进行了一次抽样调查,并根据收集的数据绘制了下面两幅不完整的统计图.请根据图中提供的信息,解答下列问题: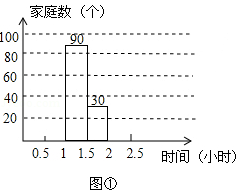

(1)本次抽样调查了多少个家庭?
(2)将图①中的条形图补充完整,直接写出用车时间的中位数落在哪个时间段内;
(3)求用车时间在1~1.5小时的部分对应的扇形圆心角的度数;
(4)若该社区有车家庭有1600个,请你估计该社区用车时间不超过1.5小时的约有多少个家庭?
(1)计算:
(2)化简分式 ,并从
,并从 中选一个你认为适合的
中选一个你认为适合的
整数 代人求值.
代人求值.
如图,在梯形ABCD中,AD∥BC,∠B=90°,BC=6,AD=3,∠DCB=30°.点E、F同时从B点出发,沿射线BC向右匀速移动.已知F点移动速度是E点移动速度的2倍,以EF为一边在CB的上方作等边△EFG.设E点移动距离为x(x>0).
⑴△EFG的边长是____(用含有x的代数式表示),当x=2时,点G的位置在_______;
⑵若△EFG与梯形ABCD重叠部分面积是y,求
①当0<x≤2时,y与x之间的函数关系式;
②当2<x≤6时,y与x之间的函数关系式;
⑶探求⑵中得到的函数y在x取何值时,存在最大值,并求出最大值.