已知抛物线C：y2=2px（p>0），曲线M：x2+2x+y2=0（y>0）．过点P（-3,0）与曲线M相切于点A的直线l，与抛物线C有且只有一个公共点B．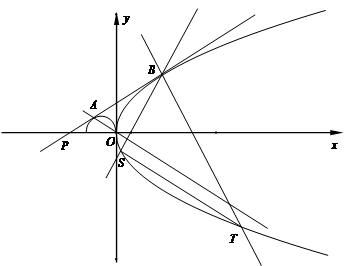
（Ⅰ）求抛物线C的方程及点A，B的坐标；
（Ⅱ）过点B作倾斜角互补的两条直线分别交抛物线C于S，T两点（不同于坐标原点），求证：直线ST∥直线AO．
.已知函数
.
（Ⅰ）求证: 对于任意的
(
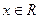)都有
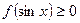恒成立
（Ⅱ）若锐角
满足
,求
.
(Ⅲ)若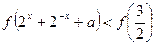
对于任意的
恒成立,求
的取值范围.
.已知函数
在一个周期内的部分函数图象如图所示.
（Ⅰ）求函数
的解析式.
（Ⅱ）求函数的单调递增区间.
(Ⅲ)求函数在区间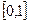
上的最大值和最小值.
若函数
.
（Ⅰ）求函数
的定义域,判断函数的奇偶性.
（Ⅱ）若关于
（
）的方程
,求.
甲盒中有1个黑球1个白球;乙盒中有1个黑球2个红球．这些
球除了颜色不同外其余无差别.
（Ⅰ）从两个盒子中各取1个球,求取出的两个球颜色不同的概率.
（Ⅱ）若把两盒中所有的球混合后放入丙盒中.从丙盒中一次取出两个球，求取出的两个球颜色不同的概率
．
（本题12分）
如图，在四棱锥P-ABCD中，侧面PAD⊥底面ABCD，侧棱PA=PD＝
，底面ABCD为直角梯形，BC∥AD,AB⊥AD,AD=2AB=2BC="2," O为AD中点.
（1）求证：PO⊥平面ABCD；
（2）求直线PB与平面PAD所成角的正弦值；
（3）线段AD上是否存在点Q，使得三棱锥
的体积为
？若存在，求出
的值；若不存在，请说明理由。