如图所示,三条直线相交于一点,求∠1+∠2+∠3的度数.
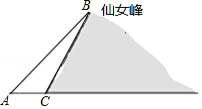
数学“综合与实践”课中,老师带领同学们来到娄底市郊区,测算如图所示的仙女峰的高度,李红盛同学利用已学的数学知识设计了一个实践方案,并实施了如下操作:先在水平地面 处测得山顶 的仰角 为 ,再由 沿水平方向前进377米到达山脚 处,测得山坡 的坡度为 ,请你求出仙女峰的高度(参考数据:
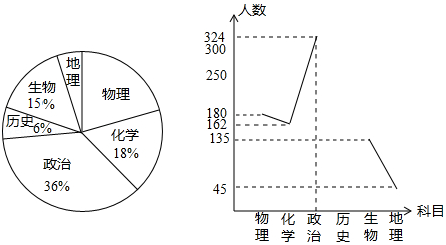
为给研究制定《中考改革实施方案》提出合理化建议,教研人员对九年级学生进行了随机抽样调查,要求被抽查的学生从物理、化学、政治、历史、生物和地理这六个选考科目中,挑选出一科作为自己的首选科目,将调查数据汇总整理后,绘制出了如图的两幅不完整的统计图,请你根据图中信息解答下列问题:
(1)被抽查的学生共有多少人?
(2)将折线统计图补充完整;
(3)我市现有九年级学生约40000人,请你估计首选科目是物理的人数.
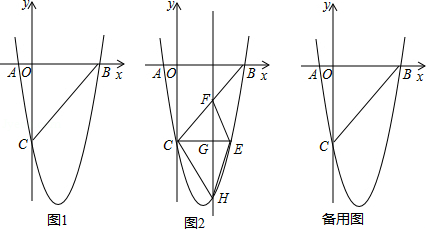
如图1,在平面直角坐标系中,已知抛物线 与 轴交于 , 两点,与 轴交于点 .
(1)求抛物线的函数表达式;
(2)若点 是 轴上的一点,且以 , , 为顶点的三角形与 相似,求点 的坐标;
(3)如图2, 轴与抛物线相交于点 ,点 是直线 下方抛物线上的动点,过点 且与 轴平行的直线与 , 分别相交于点 , ,试探究当点 运动到何处时,四边形 的面积最大,求点 的坐标及最大面积;
(4)若点 为抛物线的顶点,点 是该抛物线上的一点,在 轴, 轴上分别找点 , ,使四边形 的周长最小,求出点 , 的坐标.
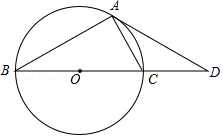
如图,已知 是 的直径,点 为 延长线上的一点,点 为圆上一点,且 , .
(1)求证: ;
(2)求证: 是 的切线.
“端午节”是我国流传了上千年的传统节日,全国各地举行了丰富多彩的纪念活动.为了继承传统,减缓学生考前的心理压力,某班学生组织了一次拔河比赛,裁判员让两队队长用“石头、剪刀、布”的手势方式选择场地位置,规则是:石头胜剪刀,剪刀胜布,布胜石头,手势相同则再决胜负.
(1)用列表或画树状图法,列出甲、乙两队手势可能出现的情况;
(2)裁判员的这种做法对甲、乙双方公平吗?请说明理由.