已知曲线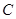 的极坐标方程为
的极坐标方程为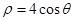 ,以极点为原点,极轴为
,以极点为原点,极轴为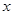 轴的正半轴建立平
轴的正半轴建立平
面直角坐标系,设直线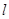 的参数方程为
的参数方程为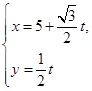 (
(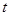 为参数)。
为参数)。
(1)求曲线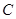 的直角坐标方程与直线
的直角坐标方程与直线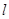 的普通方程;
的普通方程;
(2)设曲线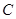 与直线
与直线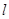 相交于
相交于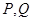 两点,以
两点,以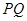 为一条边作曲线
为一条边作曲线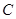 的内接矩形,求该矩形的面积。
的内接矩形,求该矩形的面积。
设函数 ,
, 的两个极值点为
的两个极值点为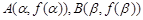 ,线段
,线段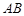 的中点为
的中点为 .
.
(1) 如果函数 为奇函数,求实数
为奇函数,求实数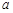 的值;当
的值;当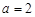 时,求函数
时,求函数 图象的对称中心;
图象的对称中心;
(2) 如果 点在第四象限,求实数
点在第四象限,求实数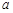 的范围;
的范围;
(3) 证明:点 也在函数
也在函数 的图象上,且
的图象上,且 为函数
为函数 图象的对称中心.
图象的对称中心.
设函数
(1)设 ,
,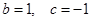 ,证明:
,证明: 在区间
在区间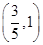 内存在唯一的零点;
内存在唯一的零点;
(2)设 为偶数,
为偶数,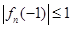 ,
, ,求
,求 的最小值和最大值;
的最小值和最大值;
(3)设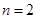 ,若对任意
,若对任意
 ,有
,有 ,求
,求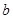 的取值范围;
的取值范围;
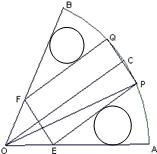
如图,在半径为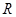 、圆心角为
、圆心角为 的扇形金属材料中剪出一个长方形
的扇形金属材料中剪出一个长方形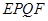 ,并且
,并且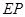 与
与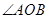 的平分线
的平分线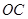 平行,设
平行,设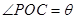 .
.
(1)试写出用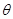 表示长方形
表示长方形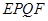 的面积
的面积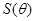 的函数;
的函数;
(2)在余下的边角料中在剪出两个圆(如图所示),试问当矩形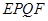 的面积最大时,能否由这个矩形和两个圆组成一个有上下底面的圆柱?如果可能,求出此时圆柱的体积.
的面积最大时,能否由这个矩形和两个圆组成一个有上下底面的圆柱?如果可能,求出此时圆柱的体积.
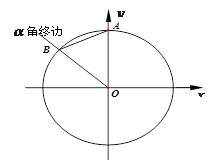
如图,单位圆(半径为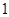 的圆)的圆心
的圆)的圆心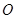 为坐标原点,单位圆与
为坐标原点,单位圆与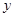 轴的正半轴交于点
轴的正半轴交于点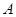 ,与钝角
,与钝角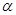 的终边
的终边 交于点
交于点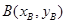 ,设
,设 .
.
(1)用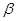 表示
表示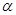 ;
;
(2)如果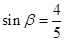 ,求点
,求点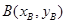 的坐标;
的坐标;
(3)求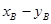 的最小值.
的最小值.
已知二次函数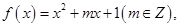 且关于
且关于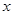 的方程
的方程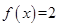 在
在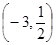 上有两个不相等的实数根.⑴求
上有两个不相等的实数根.⑴求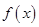 的解析式.⑵若
的解析式.⑵若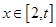 总有
总有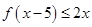 成立,求
成立,求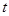 的最大值.
的最大值.