(本小题满分12分) 甲、乙两人轮流投篮,每人每次投一球,.约定甲先投且先投中者获胜,一直到有人获胜或每人都已投球3次时投篮结束.设甲每次投篮投中的概率为 ,乙每次投篮投中的概率为
,乙每次投篮投中的概率为 ,且各次投篮互不影响.
,且各次投篮互不影响.
(Ⅰ) 求甲获胜的概率;
(Ⅱ) 求投篮结束时甲的投篮次数 的分布列与期望
的分布列与期望
如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成,两相接点M、N均在直线x=5上.圆弧C1的圆心是坐标原点O,半径为r1=13;圆弧C2过点A(29,0).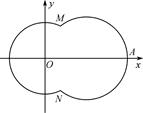
(1)求圆弧C2所在圆的方程;
(2)曲线C上是否存在点P,满足PA=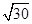 PO?若存在,指出有几个这样的点;若不存在,请说明理由;
PO?若存在,指出有几个这样的点;若不存在,请说明理由;
(3)已知直线l:x-my-14=0与曲线C交于E、F两点,当EF=33时,求坐标原点O到直线l的距离.
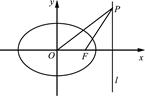
如图,在平面直角坐标系xOy中,椭圆C的中心在坐标原点O,右焦点为F.若C的右准线l的方程为x=4,离心率e=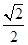 .
.
(1)求椭圆C的标准方程;
(2)设点P为准线l上一动点,且在x轴上方.圆M经过O、F、P三点,求当圆心M到x轴的距离最小时圆M的方程.
直线l过点(-4,0)且与圆(x+1)2+(y-2)2=25交于A,B两点,如果AB=8,求直线l的方程.
自点A(-3,3)发出的光线l射到x轴上,被x轴反射,反射光线所在的直线与圆C:x2+y2-4x-4y+7=0相切.求:
(1)光线l和反射光线所在的直线方程;
(2)光线自A到切点所经过的路程.
求半径为4,与圆x2+y2-4x-2y-4=0相切,且和直线y=0相切的圆的方程.