(本小题满分12分)在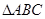 中,
中, 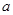 、
、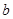 、
、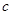 分别为内角
分别为内角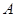 、
、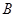 、
、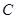 的对边,面积
的对边,面积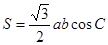 .
.
(1)求角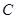 的大小;
的大小;
(2)设函数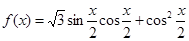 ,求
,求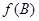 的最大值,及取得最大值时角
的最大值,及取得最大值时角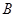 的值.
的值.
如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD, 则下列结论中不正确的是()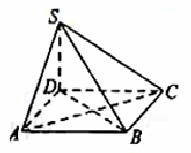
| A.AC⊥SB |
| B.AB∥平面SCD |
| C.AB与SC所成的角等于DC与SA所成的角 |
| D.SA与平面SBD所成的角等于SC与平面SBD所成的角 |
(本小题满分14分)已知函数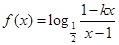 为奇函数.
为奇函数.
(1)求常数k的值;
(2)若 ,试比较
,试比较 与
与 的大小;
的大小;
(3)若函数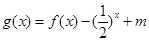 ,且
,且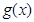 在区间
在区间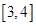 上没有零点,求实数m的取值范围.
上没有零点,求实数m的取值范围.
(本小题满分13分)已知二次函数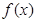 的最小值为1,且
的最小值为1,且 ,
,
(1)求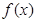 的解析式;
的解析式;
(2)若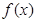 在区间
在区间 上不单调,求实数
上不单调,求实数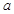 的取值范围;
的取值范围;
(3)在区间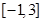 上,
上,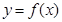 的图像恒在
的图像恒在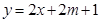 的图像上方,试确定实数
的图像上方,试确定实数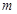 的取值范围.
的取值范围.
(本小题满分12分)某医药研究所研发了一种新药,如果成年人按规定的计量服用,据监测:服药后每毫升血液中的含药量 (微克)与时间
(微克)与时间 (时)之间近似满足如图所示的曲线。
(时)之间近似满足如图所示的曲线。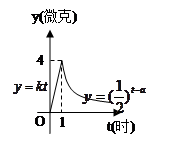
(1)写出服药后 与
与 之间的函数关系式
之间的函数关系式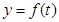 ;
;
(2)据进一步测定:每毫升血液中含药量不少于0.25微克时,治疗疾病有效。试求服药一次治疗疾病的有效时间。