(本小题满分10分)已知曲线C的参数方程为 (
(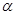 为参数),
为参数),
以直角坐标系原点为极点,Ox轴正半轴为极轴建立极坐标系.
(1)求曲线C的极坐标方程;
(2)若直线 的极坐标方程为
的极坐标方程为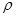 (sinθ+cosθ)=1,求直线
(sinθ+cosθ)=1,求直线 被曲线C截得的弦长.
被曲线C截得的弦长.
如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点T(-1,1)在AD边所在的直线上.
(1)求AD边,CD边所在直线的方程;
(2)求矩形ABCD外接圆的方程.
已知y=2x是△ABC中∠C的内角平分线所在直线的方程,若A(﹣4,2),B(3,1).
(1)求点A关于y=2x的对称点P的坐标;
(2)求直线BC的方程;
(3)判断△ABC的形状.
已知圆M的方程为x 2+(y-2)2=1,直线l的方程为x-2y=0,点P在直线l上,过P点作圆M的切线PA,PB,切点为A,B.
(1)若∠APB=60°,试求点P的坐标;
(2)若P点的坐标为(2,1),过P作直线与圆M交于C,D两点,当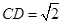 时,求直线CD的方程;
时,求直线CD的方程;
(3)求证:经过A,P,M三点的圆必过定点,并求出所有定点的坐标.
已知方程x 2+y 2-2x-4y+m=0.
(1)若此方程表示圆,求m的取值范围;
(2)若(1)中的圆与直线x+2y-4=0相交于M,N两点,且 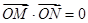 (其中O为坐标原点)求m的值;
(其中O为坐标原点)求m的值;
(3)在(2)的条件下,求以MN为直径的圆的方程.
已知两圆x 2+y 2-2x-6y-1=0.x 2+y 2-10x-12y+m=0.
(1)m取何值时两圆外切?
(2)m取何值时两圆内切?
(3)当m=45时,求两圆的公共弦所在直线的方程和公共弦的长.