已知横坐标为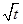 的点
的点 在曲线
在曲线 :
: 上,曲线
上,曲线 在点
在点 处的切线与直线
处的切线与直线 交于点
交于点 ,与
,与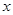 轴交于点
轴交于点 .设点
.设点 ,
, 的横坐标分别为
的横坐标分别为 ,记
,记 .正数数列
.正数数列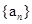 满足
满足 ,
,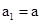 .
.
(Ⅰ)写出 之间的关系式;
之间的关系式;
(Ⅱ)若数列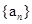 为递减数列,求实数
为递减数列,求实数 的取值范围;
的取值范围;
(Ⅲ)若 ,设数列
,设数列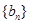 的前
的前 项和为
项和为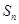 ,求证:
,求证: .
.
下列命题中为真命题的是()
| A.命题“若x>1,则x2>1”的否命题 |
| B.命题“若x>y,则|x|>y”的逆命题 |
C.若k<5,则两椭圆 与 与 有不同的焦点 有不同的焦点 |
| D.命题“若方程x2+ky2=2表示焦点在y轴上的椭圆,则k的取值范围为(0,1)”的逆否命题 |
已知函数f(x)=alnx+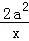 +x(a≠0).
+x(a≠0).
(Ⅰ)若曲线y=f(x)在点(1,f(1))处的切线与直线x﹣2y=0垂直,求实数a的值;
(Ⅱ)讨论函数f(x)的单调性;
(Ⅲ)当a∈(﹣∞,0)时,记函数f(x)的最小值为g(a),求证:g(a)≤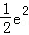 .
.
已知对称中心为坐标原点的椭圆C1与抛物线C2:x2=4y有一个相同的焦点F1,直线l:y=2x+m与抛物线C2只有一个公共点.
(1)求直线l的方程;
(2)若椭圆C1经过直线l上的点P,当椭圆C1的离心率取得最大值时,求椭圆C1的方程及点P的坐标.
通过随机询问某校高二年级学生在购买食物时是否看营养说明,得到如下列联表:
| 男生 |
女生 |
总计 |
|
| 看营养说明 |
50 |
30 |
80 |
| 不看营养说明 |
10 |
x |
y |
| 总计 |
60 |
z |
110 |
参考数据:
| P(K2≥K) |
0.10 |
0.05 |
0.01 |
0.005 |
| K |
2.706 |
3.841 |
6.635 |
7.879 |
参考公式:K2=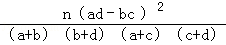 ,n=a+b+c+d
,n=a+b+c+d
(1)写出x,y,z的值
(2)根据以上列联表,问有多大把握认为“性别在购买食物时看营养说明”有关?
(3)从女生中按是否看营养说明采取分层抽样,抽取容量为5的样本,再从这5名女生中随机选取两名作深度访谈.求选到看与不看营养说明的女生各一名的概率.
已知数列{an}满足a1=1,(n+1)an+1=nan(n∈N*).
(1)求{an}的通项公式.
(2)若bn= an,数列{bn}的前n项和为Tn,求证:Tn<2.
an,数列{bn}的前n项和为Tn,求证:Tn<2.