某工厂投入生产一种机器的总成本为2000万元．当该机器生产数量至少为10台，但不超过70台时，每台成本y与生产数量x之间是一次函数关系，函数y与自变量x的部分对应值如下表：
| x/台 |
10 |
20 |
30 |
| y/（万元·台－1） |
60 |
55 |
50 |
（1）求y与x之间的函数关系式，并写出自变量x的取值范围；
（2）求该机器的生产数量；
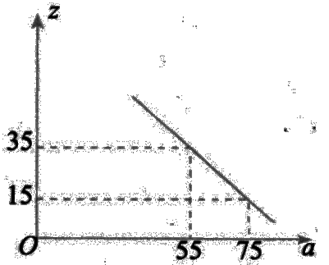
（3）市场调查发现，这种机器每月销售量z（台）与售价a（万元／台）之间满足如图所示的函数关系，该厂生产这种机器后第一个月按同一售价共卖出这种机器25台，请你求出该厂第一个月销售这种机器的利润．（注：利润＝售价－成本）
（本小题满分6分）如图二次函数y=
+bx+c的图象经过A（－1,0）和B（3,0）两点，且交
轴于点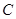
．
（1）试确定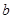
、
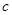的值；
（2）过点C作CD∥x轴轴交抛物线于点D点M为此抛物线的顶点，试确定△MCD的形状．
参考公式：顶点坐标（
）
如图，已知点A（3，0），以A为圆心作⊙A与Y轴切于原点，与x轴的另一个交点为B，过B作⊙A的切线l．
（1）以直线l为对称轴的抛物线过点A及点C（0，9），求此抛物线的解析式；
（2）抛物线与x轴的另一个交点为D，过D作⊙A的切线DE，E为切点，求DE的长；
（3）点F是切线DE上的一个动点，当△BFD与△EAD相似时，求出BF的长 ．
为了落实国家的惠农政策，某地政府制定了农户投资购买收割机的补贴办法，其中购买Ⅰ、Ⅱ两型收割机所投资的金额与政府补贴的额度存在下表所示的函数对应关系：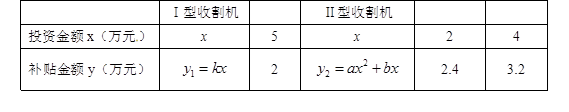
（1）分别求出
和
的函数表达式；
（2）旺叔准备投资10万元购买Ⅰ、Ⅱ两型收割机．请你设计一个能获得最大补贴金额的方案，并求出按此方案能获得的补贴金额．
如图，已知二次函数
的图像经过A（－1，－1），C（1，3）.
（1）求二次函数的解析式并画出它的图像；
（2）直接写出点A关于抛物线对称轴的对称点A'的坐标；
（3）求该抛物线上到x轴的距离为2的所有点的坐标．
如图所示，二次函数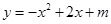
的图象与x轴的一个交点为A（3，0），另一个交点为B，且与y轴交于点C．
（1）求m的值；
（2）求点B的坐标；
（3）该二次函数图像上有一点D（x，y）（其中
，
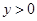），使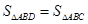
，求点D的坐标．