如图所示,已知一次函数y=2x+a与y=-x+b的图象都经过点A(-2,0),且与y轴分别交于B,C两点,求△ABC的面积.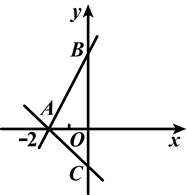
(年贵州省黔南州)如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=2,AE=3,tan∠BOD= .
.
(1)求⊙O的半径OD;
(2)求证:AE是⊙O的切线;
(3)求图中两部分阴影面积的和.
(年贵州省铜仁市)如图,已知三角形ABC的边AB是⊙O的切线,切点为B.AC经过圆心O并与圆相交于点D、C,过C作直线CE丄AB,交AB的延长线于点E.
(1)求证:CB平分∠ACE;
(2)若BE=3,CE=4,求⊙O的半径.
(年贵州省贵阳市)如图,在矩形纸片ABCD中,AB=4,AD=12,将矩形纸片折叠,使点C落在AD边上的点M处,折痕为PE,此时PD=3.
(1)求MP的值;
(2)在AB边上有一个动点F,且不与点A,B重合.当AF等于多少时,△MEF的周长最小?
(3)若点G,Q是AB边上的两个动点,且不与点A,B重合,GQ=2.当四边形MEQG的周长最小时,求最小周长值.(计算结果保留根号)
(年贵州省毕节)如图,将▱ABCD的AD边延长至点E,使DE= AD,连接CE,F是BC边的中点,连接FD.
AD,连接CE,F是BC边的中点,连接FD.
(1)求证:四边形CEDF是平行四边形;
(2)若AB=3,AD=4,∠A=60°,求CE的长.
(年贵州省贵阳市)如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,且AE∥CD,CE∥AB.
(1)四边形ADCE是菱形;
(2)若∠B=60°,BC=6,求菱形ADCE的高.(计算结果保留根号)