(本小题满分14分)如图,四边形OMTN中,OM=ON,TM=TN,我们把这种两组邻边分别相等的四边形叫做筝形.
(1)试探究筝形对角线之间的位置关系,并证明你的结论;
(2)在筝形ABCD中,已知AB=AD=5,BC=CD,BC>AB,BD,AC为对角线,BD=8.
①是否存在一个圆使得A,B,C,D四个点都在这个圆上?若存在,求出圆的半径;若不存在, 请说明理由;
②过点B作BF⊥CD,垂足为F,BF交AC于点E,连接DE.当四边形ABED为菱形时,求点F到AB 的距离.
第20届世界杯足球赛正在如火如荼的进行,爸爸想通过一个游戏决定小明能否看今晚的比赛:在一个不透明的盒子中放入三张卡片,每张卡片上写着一个实数,分别为3,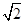 , 2
, 2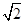 (每张卡片除了上面的实数不同以外其余均相同),爸爸让小明从中任意取一张卡片,如果抽到的卡片上的数是有理数,就让小明看比赛,否则就不能看.
(每张卡片除了上面的实数不同以外其余均相同),爸爸让小明从中任意取一张卡片,如果抽到的卡片上的数是有理数,就让小明看比赛,否则就不能看.
(1)请你直接写出按照爸爸的规则小明能看比赛的概率;
(2)小明想了想,和爸爸重新约定游戏规则:自己从盒子中随机抽取两次,每次抽取一张卡片,第一次抽取后记下卡片上的数,再将卡片放回盒中抽取第二次,如果抽取的两数之积是有理数,自己就看比赛,否则就不看.请你用列表法或树状图法求出按照此规则小明看比赛的概率.
(1)已知:如图,点A,C,D,B在同一条直线上,AC=BD,AE=BF,∠A=∠B.求证:∠E=∠F.
(2)如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上).请你根据他们测量数据计算这棵树CD的高度(结果精确到0.1m).(参考数据: ≈1.414,
≈1.414, ≈1.732)
≈1.732)
如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,-1),并且与y轴交于点C(0,3),与x轴交于两点A,B.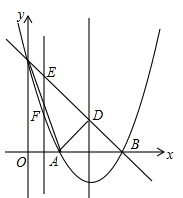
(1)求抛物线的表达式;
(2)点E为直线BC上一动点,过点E作y轴的平行线EF,与抛物线交于点F.问是否存在点E,使得以D、E、F为顶点的三角形与△BCO相似?若存在,求出点E的坐标;若不存在,请说明理由.
如图所示,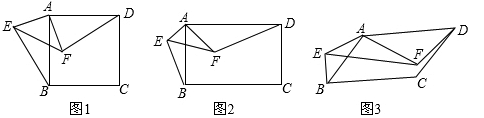
(1)正方形ABCD及等腰Rt△AEF有公共顶点A,∠EAF=90°,连接BE、DF.将Rt△AEF绕点A旋转,在旋转过程中,BE、DF具有怎样的数量关系和位置关系?结合图(1)给予证明;
(2)将(1)中的正方形ABCD变为矩形ABCD,等腰Rt△AEF变为Rt△AEF,且AD=kAB,AF=kAE,其他条件不变.(1)中的结论是否发生变化?结合图(2)说明理由;
(3)将(2)中的矩形ABCD变为平行四边形ABCD,将Rt△AEF变为△AEF,且∠BAD=∠EAF=a,其他条件不变.(2)中的结论是否发生变化?结合图(3),如果不变,直接写出结论;如果变化,直接用k表示出线段BE、DF的数量关系,用a表示出直线BE、DF形成的锐角β.
学校举办一项小制作评比活动.作品上交时限为3月1日至30日,组委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的作品件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1.第三组的件数是12.
请你回答:
(1)本次活动共有件作品参赛;各组作品件数的众数是件;
(2)经评比,第四组和第六组分别有10件和2件作品获奖,那么你认为这两组中哪个组获奖率较高?为什么?
(3)小制作评比结束后,组委会决定从4件最优秀的作品A、B、C、D中选出两件进行全校展示,请用树状图或列表法求出刚好展示作品B、D的概率.