(本小题满分15分)已知数列 是公差不为零的等差数列,
是公差不为零的等差数列, ,且
,且 成等比数列.
成等比数列.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设数列 满足:
满足: ,
,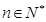 ,令
,令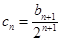 ,
,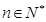 ,求数列
,求数列 的前
的前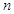 项和
项和 .
.
已知函数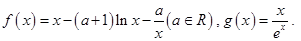
(I)求f(x)的单调区间;
(II)当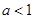 时,若存在
时,若存在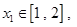 使得对任意的
使得对任意的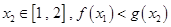 恒成立,求
恒成立,求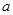 的取值范围。
的取值范围。
从某学校高三年级男生随机抽取若干名测量身高,发现测量数据全部介于155cm和195cm之间且每个男生被抽取到的概率为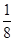 ,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),┅,第八组[190,195),右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组的频数均为4,第六组,第七组,第八组的频率依次构成等差数列。
,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),┅,第八组[190,195),右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组的频数均为4,第六组,第七组,第八组的频率依次构成等差数列。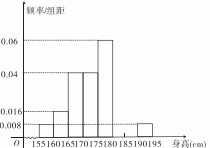
(I)补充完整频率分布直方图,并估计该校高三年级全体男生身高不低于180cm的人数;
(II)从最后三组中任取2名学生参加学校篮球队,求他们来自不同组的事件概率。
已知△ABC的内角A,B,C所对的边分别是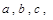 且对
且对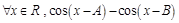 是常数,
是常数,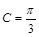 .
.
(1)求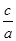 的值;
的值;
(2)若边长c=2,解关于x的不等式asinx-bcosx<2。
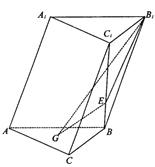
如图,在斜三棱柱 中,侧面
中,侧面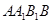 ⊥底面
⊥底面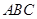 ,侧棱
,侧棱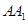 与底面
与底面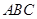 成
成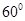 的角,
的角,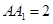 .底面
.底面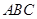 是边长为2的正三角形,其重心为
是边长为2的正三角形,其重心为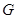 点,
点, 是线段
是线段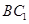 上一点,且
上一点,且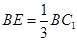 .
.
(Ⅰ)求证: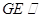 //侧面
//侧面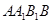 ;
;
(Ⅱ)求平面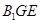 与底面
与底面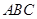 所成锐二面角的正切值.
所成锐二面角的正切值.
已知等差数列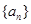 的前
的前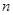 项和为
项和为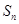 ,且
,且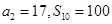 .
.
(Ⅰ)求数列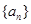 的通项公式;
的通项公式;
(Ⅱ)若数列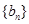 满足
满足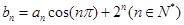 ,求数列
,求数列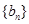 的前
的前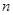 项和.
项和.