某玉米种子的价格为a元/千克，如果一次购买2千克以上的种子，超过2千克部分的种子价格打8折．某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析，并绘制出了函数图象．以下是该科技人员绘制的图象和表格的不完整资料，已知点A的坐标为（2，10）．请你结合表格和图象：
| 付款金额（元） |
a |
7．5 |
10 |
12 |
b |
| 购买量（千克） |
1 |
1．5 |
2 |
2．5 |
3 |
（1）指出付款金额和购买量哪个变量是函数的自变量x，并写出表中a、b的值；
（2）求出当x＞2时，y关于x的函数解析式；
（3）甲农户将8．8元钱全部用于购买该玉米种子，乙农户购买了4165克该玉米种子，分别计算他们的购买量和付款金额．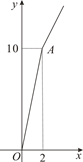
先化简，再求值．
，其中 x=tan600+2 ．
如图，矩形ABOD的两边OB，OD都在坐标轴的正半轴上，OD＝3，另两边与反比例函数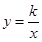
(k≠0)的图象分别相交于点E、F，且DE＝2．过点E作EH⊥x轴于点H，过点F作FG⊥EH于点G．回答下面的问题：
(1)①求反比例函数的解析式．
②当四边形AEGF为正方形时，求点F的坐标．
(2)小亮进一步研究四边形AEGF的特征后提出问题：“当AE＞EG时，矩形AEGF与矩形DOHE能否全等？能否相似？”
针对小亮提出的问题，请你判断这两个矩形能否全等(直接写出结论即可)．这两个矩形能否相似？若能相似，求出相似比；若不能相似，试说明理由．
如图，在△ABC中，D是BC边上的点(不与点B，C重合)，连接AD．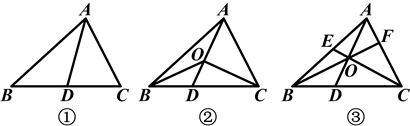
问题引入：
(1)如图①，当点D是BC边上的中点时，S△ABD︰S△ABC＝________；当点D是BC边上任意一点时，S△ABD︰S△ABC＝________(用图中已有线段表示)．
探索研究：
(2)如图②，在△ABC中，O点是线段AD上的一点(不与点A，D重合)，连接BO，CO，试猜想S△BOC与S△ABC之比应该等于图中哪两条线段之比，并说明理由．
拓展应用：
(3)如图③，O是线段AD上一点(不与点A，D重合)，连接BO并延长交AC于点F，连接CO并延长交AB于点E，试猜想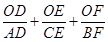
的值，并说明理由．
如图，双曲线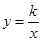
(x＞0)经过△OAB的顶点A和OB的中点C，AB∥x轴，点A的坐标为(2，3)．
(1)求k的值；
(2)若点D(3，m)在双曲线上，求直线AD的解析式；
(3)计算△OAB的面积．
已知A(x1，y1)，B(x2，y2)是反比例函数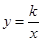
的图象上的两点，且x1－x2＝－2，x1·x2＝3，
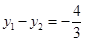，当－3＜x＜－1时，求y的取值范围．