(本小题满分6分)
小颖和小丽做“摸球”游戏:在一个不透明的袋子中装有编号为1~4的四个球(除编号外都相同),从中随机摸出一个球,记下数字后放回,再从中摸出一个球,记下数字。若两次数字之和大于5,则小颖胜,否则小丽胜。这个游戏对双方公平吗?请说明理由。
某书店参加某校读书活动,并为每班准备了A,B两套名著,赠予各班甲、乙两名优秀读者,以资鼓励.某班决定采用游戏方式发放,其规则如下:将三张除了数字2,5,6不同外其余均相同的扑克牌,数字朝下随机平铺于桌面,从中任取2张,若牌面数字之和为偶数,则甲获A名著;若牌面数字之和为奇数,则乙获得A名著,你认为此规则合理吗?为什么?
先化简再求值: ,其中a=5,b=2.
,其中a=5,b=2.
求不等式组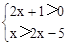 的正整数解.
的正整数解.
计算; .
.
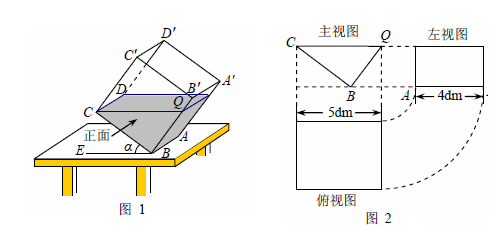
一透明的敞口正方体容器ABCD -A′B′C′D′ 装有一些液体,棱AB始终在水平桌面上,容器底部的倾斜角为α (∠CBE = α,如图1所示).
探究 如图1,液面刚好过棱CD,并与棱BB′ 交于点Q,此时液体的形状为直三棱柱,其三视图及尺寸如
图2所示.解决问题:
(1)CQ与BE的位置关系是,BQ的长是dm;
(2)求液体的体积;(参考算法:直棱柱体积V液 = 底面积SBCQ×高AB)
(3)求α的度数.(注:sin49°=cos41°=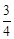 ,tan37°=
,tan37°=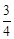 )
)
拓展 在图1的基础上,以棱AB为轴将容器向左或向右旋转,但不能使液体溢出,图3或图4是其正面示意图.若液面与棱C′C或CB交于点P,设PC = x,BQ = y.分别就图3和图4求y与x的函数关系式,并写出相应的α的范围.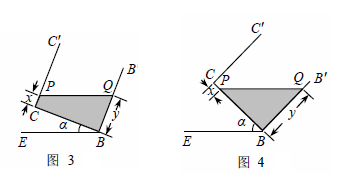
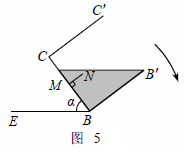
延伸 在图4的基础上,于容器底部正中间位置,嵌入一平行于侧面的长方形隔板(厚度忽略不计),得到图5,隔板高NM =" 1" dm,BM = CM,NM⊥BC.继续向右缓慢旋转,当α = 60°时,通过计算,判断溢出容器的液体能否达到4 dm3.