六人按下列要求站一横排,分别有多少种不同的站法?
(l)甲不站两端;
(2)甲、乙必须相邻;
(3)甲、乙不相邻;
(4)甲、乙之间间隔两人;
(5)甲不站左端,乙不站右端.
已知圆M的圆心M在x轴上,半径为1,直线 :y=
:y= x-
x-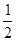 被圆M所截的弦长为
被圆M所截的弦长为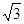 ,且圆心M在直线
,且圆心M在直线 的下方.
的下方.
(1)求圆M的方程;
(2)设A(0,t),B(0,t+6)(-5≤t≤-2),若圆M是△ABC的内切圆,求△ABC的面积S的最大值和最小值.
袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为 ,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时即终止.每个球在每一次被取出的机会是等可能的.用
,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时即终止.每个球在每一次被取出的机会是等可能的.用 表示取球终止时所需要的取球次数.
表示取球终止时所需要的取球次数.
(1)求袋中原有白球的个数;
(2)求随机变量 的概率分布;
的概率分布;
(3)求甲取到白球的概率.
已知三棱柱ABC-A′B′C′中,平面BCC′B′⊥底面ABC,BB′⊥AC,底面ABC是边长为2的等边三角形,AA′=3,E、F分别在棱AA′,CC′上,且AE=C′F=2.
(1) 求证:BB′⊥底面ABC;
(2)在棱A′B′上是否存在一点M,使得C′M∥平面BEF,若存在,求 值,若不存在,说明理由
值,若不存在,说明理由
(3)求棱锥 -BEF的体积
-BEF的体积
某市政府为了确定一个较为合理的居民用电标准,必须先了解全市居民日常用电量的分布情况.现采用抽样调查的方式,获得了n位居民在2012年的月均用电量(单位:度)数据,样本统计结果如下图表:
| 分组 |
频 数 |
频 率 |
| [0, 10) |
0.05 |
|
| [10,20) |
0.10 |
|
| [20,30) |
30 |
|
| [30,40) |
0.25 |
|
| [40,50) |
0.15 |
|
| [50,60] |
15 |
|
| 合计 |
n |
1 |
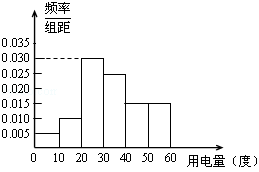
(1)求月均用电量的中位数与平均数估计值;
(2)如果用分层抽样的方法从这n位居民中抽取8位居民,再从这8位居民中选2位居民,那么至少有1位居民月均用电量在30至40度的概率是多少?
(3)用样本估计总体,把频率视为概率,从这个城市随机抽取3位居民(看作有放回的抽样),求月均用电量在30至40度的居民数X的分布列.
一个盒子里装有三张卡片,分别标记有数字1,2,3,这三张卡片除标记的数字外完全相同.随机有放回地抽取3次,每次抽取1张,将抽取的卡片上的数字依次记为a,b,c.
(1)求“抽取的卡片上的数字满足a+b=c”的概率;
(2)求“抽取的卡片上的数字a,b,c不完全相同”的概率.