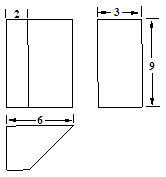某工厂根据市场需求,计划生产A、B两种型号挖掘机共100台,该厂所筹生产资金不少于22400万元,但不超过22500万元,所生产两型号挖掘机可全部售出,两型号挖掘机生产成本和售价如下表:
| 型号 |
A |
B |
| 成本(万元/台) |
200 |
240 |
| 售价(万元/台) |
250 |
300 |
(1)该厂对这两型挖掘机有哪几种生产方案?
(2)该厂如何生产能获得最大利润?
(3)根据市场调查,每台B型挖掘机的售价不会改变,每台A型挖掘机的售价将会提高m万元(m>0),该厂应该如何生产可以获得最大利润?(注:利润=售价-成本)
如图,△ABC中,∠C=Rt∠,AB=5cm,BC=3cm,若动点P从点C开始,按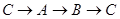 的路径运动,且速度为每秒1㎝,设出发的时间为t秒.
的路径运动,且速度为每秒1㎝,设出发的时间为t秒.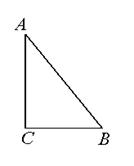
(1)出发2秒后,求△ABP的周长.
(2)问t为何值时,△BCP为等腰三角形?
(3)另有一点Q,从点C开始,按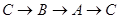 的路径运动,且速度为每秒2㎝,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动。当t为何值时,直线PQ把△ABC的周长分成相等的两部分?(其中(3)直接写出答案即可)
的路径运动,且速度为每秒2㎝,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动。当t为何值时,直线PQ把△ABC的周长分成相等的两部分?(其中(3)直接写出答案即可)
如图,等边 中,D是AB边上的动点,以CD为一边,向上作等边
中,D是AB边上的动点,以CD为一边,向上作等边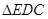 ,连结AE。
,连结AE。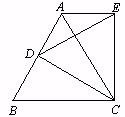
(1)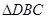 和
和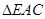 会全等吗?请说说你的理由。
会全等吗?请说说你的理由。
(2)试说明AE∥BC的理由.
在同一平面内,如果有两条直线都与第三条直线垂直,那么这两条直线的位置关系是。(填“垂直”或“平行”)
某市篮球队到学校选拔一名队员.教练对王亮和李刚两名同学进行5次3分投篮测试,每人每次投10个球,下图记录的是这两名同学5次投篮中所投中的个数.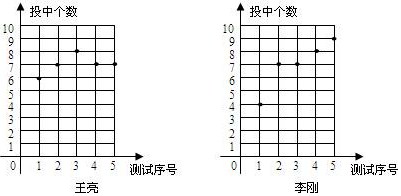
(1)请你根据图中的数据,填写下表.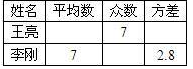
(2)你认为谁的成绩比较稳定,为什么?
(3)若你是教练,你打算选谁?简要说明理由
如图所示是一个几何体的三视图。求该几何体的侧面积(长度单位cm)。