发现问题:
如图(1),在ΔABC中,∠A=2∠B,且∠A=60°.
我们可以进行以下计算:
由题意可知:∠B=30°,∠C=90°,
可得到:c=2b,a= b,
b,
所以a2-b2=( b)2-b2=2b2=b·c.
b)2-b2=2b2=b·c.
即a2-b2= bc.
提出猜想:
对于任意的ΔABC,当∠A=2∠B时,关系式a2-b2=bc都成立.
验证猜想:
(1)(验证特殊三角形)如图(2),请你参照上述研究方法,对等腰直角三角形进行验证,判断猜想是否正确,并写出验证过程;
已知:ΔABC中,∠A=2∠B,∠A=90°求证:a2-b2=bc.
(2)(验证一般三角形)如图(3),
已知:ΔABC中,∠A=2∠B,求证:a2-b2= bc.
结论应用:
若一个三角形的三边长恰为三个连续偶数,且∠A=2∠B,请直接写出这个三角形三边的长,不必说明理由.
随着车辆的增加,交通违规的现象越来越严重,交警对某雷达测速区检测到的一组汽车的时速(千米/时)数据进行整理,得到其频数及频率如表(未完成):
| 数据段 |
频数 |
频率 |
| 30﹣40 |
10 |
0.05 |
| 40﹣50 |
36 |
|
| 50﹣60 |
0.39 |
|
| 60﹣70 |
||
| 70﹣80 |
20 |
0.10 |
| 总计 |
200 |
1 |
(1)请你把表中的数据填写完整;
(2)补全频数分布直方图;
(3)如果汽车时速不低于60千米即为违章,则违章车辆共有多少辆?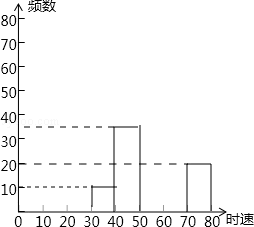
画出四边形ABCD关于O点成中心对称的四边形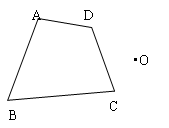
“中国竹乡”安吉县有着丰富的毛竹资源,某企业已收购毛竹52.5吨,根据市场信息,如果将毛竹直接销售,每吨课获利100元;如果对毛竹进行粗加工,每天可加工8吨,每吨可获利1000元;如果对毛竹进行精加工,每天可加工0.5吨,每吨可获利5000元,由于条件限制,在同一天中只能采用一种方式加工,并且必须在一个月(30天)将这批毛竹全部销售,为此研究了两种方案:
方案一:将毛竹全部进行粗加工后销售。
方案二:30天时间全部进行精加工,未来得及加工的毛竹在市场上直接销售。
试计算方案一、方案二所获得的利润。
是否存在第三种方案,将部分毛竹粗加工,其余毛竹精加工,并且恰好在30天内完成?若存在,求销售后所获得的利润;若不存在,请说明理由。
一张方桌由一个桌面,四个桌腿组成,如果1立方米木料可以做方桌的桌面50个或做桌腿300条,现有5立方米木料,那么用多少立方米木料做桌面,多少立方米做桌腿,恰好能配成方桌?
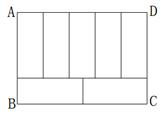
如图:周长为68的长方形ABCD被分成7个形状、大小完全一样的长方形,则ABCD的面积是多少?