(本小题满分10分)已知AC,EC分别为四边形ABCD和EFCG的对角线,点E在△ABC内,∠CAE+∠CBE=90.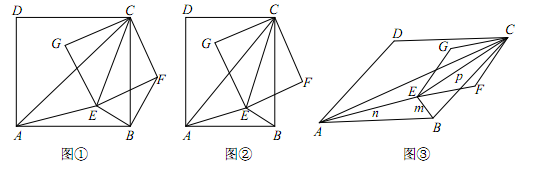
(1)如图①,当四边形ABCD和EFCG均为正方形时,连接BF.
i)求证:△CAE∽△CBF;
ii)若BE=1,AE=2,求CE的长;
(2)如图②,当四边形ABCD和EFCG均为矩形,且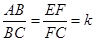 时,若BE=1,AE=2,CE=3,求k的值;
时,若BE=1,AE=2,CE=3,求k的值;
(3)如图③,当四边形ABCD和EFCG均为菱形,且∠DAB=∠GEF=45°时,设BE=m,AE=n,CE=p,试探究m,n,p三者之间满足的等量关系.(直接写出结果,不必写出解答过程)
用适当方法解下列方程
(1)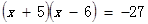
(2)
计算
(1)
(2)化简求值: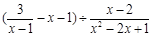 ,其中x=-
,其中x=-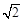
如图1,矩形ABCD中,AB=21,AD=12,E是CD边上的一点,CE=5,M是BC边上的中点,动点P从点A出发,沿AB边以每秒1个单位长度的速度向终点B运动,连结PM.设动点P的运动时间是t秒.
(1)求线段AE的长;
(2)当△ADE与△PBM相似时,求t的值;
(3)如图2,连接EP,过点P作PH⊥AE于H.①当EP平分四边形PMEH的面积时,求t的值;②以PE为对称轴作线段BC的轴对称图形B′C′,当线段B′C′与线段AE有公共点时,写出t的取值范围(直接写出答案).
如图,在平面直角坐标系的第一象限中,有一各边所在直线均平行于坐标轴的矩形ABCD,且点A在反比例函数L1:y=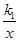 (x>0) 的图象上,点C在反比例函数L2:y=
(x>0) 的图象上,点C在反比例函数L2:y=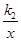 (x>0) 的图象上(矩形ABCD夹在L1与L2之间).(1)若点A坐标为(1,1)时,则L1的解析式为.(2)在(1)的条件下,若矩形ABCD是边长为1的正方形,求L2的解析式.(3)若k1=1,k2=6,且矩形ABCD的相邻两边分别为1和2,求符合条件的顶点C的坐标.
(x>0) 的图象上(矩形ABCD夹在L1与L2之间).(1)若点A坐标为(1,1)时,则L1的解析式为.(2)在(1)的条件下,若矩形ABCD是边长为1的正方形,求L2的解析式.(3)若k1=1,k2=6,且矩形ABCD的相邻两边分别为1和2,求符合条件的顶点C的坐标.
为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式.
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?