(本小题满分13分)如图,直角坐标系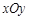 中,一直角三角形
中,一直角三角形 ,
,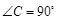 ,
,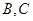 在
在 轴上且关于原点
轴上且关于原点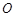 对称,
对称,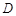 在边
在边 上,
上, ,
,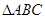 的周长为12.若一双曲线
的周长为12.若一双曲线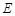 以
以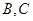 为焦点,且经过
为焦点,且经过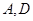 两点.
两点.
(1)求双曲线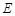 的方程;
的方程;
(2)若一过点 (
( 为非零常数)的直线
为非零常数)的直线 与双曲线
与双曲线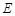 相交于不同于双曲线顶点的两点
相交于不同于双曲线顶点的两点 、
、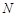 ,且
,且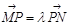 ,问在
,问在 轴上是否存在定点
轴上是否存在定点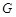 ,使
,使 ?若存在,求出所有这样定点
?若存在,求出所有这样定点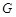 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
如图:已知直三棱柱ABC—A1B1C1,AB=AC,F为棱BB1上一点,BF∶FB1=2∶1,BF=BC=2a。
(I)若D为BC的中点,E为AD上不同于A、D的任意一点,证明EF⊥FC1;
(II)试问:若AB=2a,在线段AD上的E点能否使EF与平面BB1C1C成60°角,为什么?证明你的结论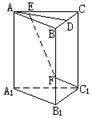
如图,在正三棱柱ABC—A1B1C1中,各棱长都相等,D、E分别为AC1,BB1的中点。(1)求证:DE∥平面A1B1C1;(2)求二面角A1—DE—B1的大小。
如图,直角梯形ABCE中,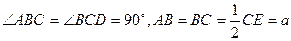 ,D是CE的中点,点M和点N在
,D是CE的中点,点M和点N在 ADE绕AD向上翻折的过程中,分别以
ADE绕AD向上翻折的过程中,分别以 的速度,同时从点A和点B沿AE和BD各自匀速行进,t 为行进时间,0
的速度,同时从点A和点B沿AE和BD各自匀速行进,t 为行进时间,0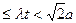 。
。
(1)求直线AE与平面CDE所成的角;
(2)求证:MN//平面CDE。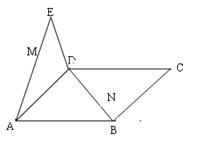
如图,直三棱柱ABC-A1B1C1的底面ABC为等腰直角三角形,∠ACB=900,AC=1,C点到AB1的距离为CE=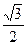 ,D为AB的中点.
,D为AB的中点.
(1)求证:AB1⊥平面CED;
(2)求异面直线AB1与CD之间的距离;
(3)求二面角B1—AC—B的平面角.
如图,几何体ABCDE中,△ABC是正三角形,EA和DC都垂直于平面ABC,且EA=AB=2a,DC=a,F、G分别为EB和AB的中点.
(1)求证:FD∥平面ABC;
(2)求证:AF⊥BD;
(3) 求二面角B—FC—G的正切值.