在平面直角坐标系中,等边三角形OAB的边长是2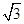 ,且OB边落在x轴的正半轴上,点A落在第一象限.将△OAB沿直线y=kx+b折叠,使点A落在x轴上,设点C是点A落在x轴上的对应点.
,且OB边落在x轴的正半轴上,点A落在第一象限.将△OAB沿直线y=kx+b折叠,使点A落在x轴上,设点C是点A落在x轴上的对应点.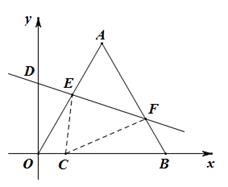
(1)如果点A恰好落在点C(0,0),求b的值;
(2)设点C的横坐标为m,求b与m之间的函数关系式;
(3)直接写出当b= 时,点C的坐标。
时,点C的坐标。
图①是一个长为 、宽为
、宽为 的长方形,用这样四个全等的长方形,拼成如图②的正方形.
的长方形,用这样四个全等的长方形,拼成如图②的正方形.
(1)按要求填空:
ⅰ.请用含字母 、
、 的代数式表示图②中的阴影部分的正方形的边长: ;
的代数式表示图②中的阴影部分的正方形的边长: ;
ⅱ.请用含字母 、
、 的代数式,用两种不同的方法表示图②中阴影部分的面积:
的代数式,用两种不同的方法表示图②中阴影部分的面积:
方法1:
方法2:
ⅲ.观察图②,请写出代数式 、
、 、
、 之间的等量关系: ;
之间的等量关系: ;
(2)根据(1)题中的等量关系,解决如下问题:
若 ,
, ,求
,求 的值.
的值.
先化简,再求值: ,其中
,其中 ,
, 满足
满足 .
.
(1)解方程: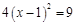
(2)分解因式: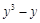
数学思想运用:
(1)如图①所示,△ABC的外角平分线交于G,若∠A=80°,则∠BGC= °,请你猜测∠BGC和∠A的数量关系: .
(2)如图②所示,若△ABC的内角平分线交于点I,若∠A=50°,则∠BIC= °,请你猜测∠BIC和∠A的数量关系: .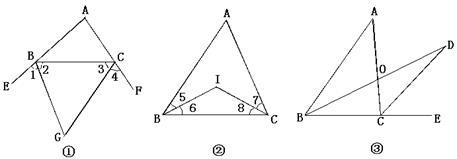
(3)已知,如图③,△ABC中,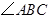 的平分线与
的平分线与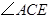 的平分线交于
的平分线交于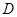 点,请你猜测∠D和∠A的数量关系: .
点,请你猜测∠D和∠A的数量关系: .
若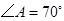 ,求
,求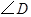 的度数(写出求解过程).
的度数(写出求解过程).
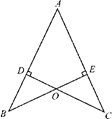
如图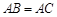 ,
,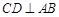 于点
于点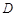 ,
,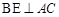 于点E,
于点E,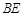 与
与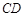 相交于点
相交于点 .
.
(1)求证: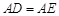 ;
;
(2)连接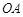 ,
,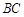 ,试判断直线
,试判断直线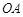 ,
,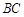 的位置关系,并说明理由.
的位置关系,并说明理由.