如图,把含有30°角的三角板ABO置入平面直角坐标系中,A,B两点坐标分别为(3,0)和(0,3 ).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动的面四民﹒数学兴趣小组对捐款情况进行了抽样调查,速度分别为1,
).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动的面四民﹒数学兴趣小组对捐款情况进行了抽样调查,速度分别为1, ,2 (长度单位/秒)﹒一直尺的上边缘l从x轴的位置开始以
,2 (长度单位/秒)﹒一直尺的上边缘l从x轴的位置开始以 (长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.
(长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.
请解答下列问题:
(1)过A,B两点的直线解析式是 ;
(2)当t﹦4时,点P的坐标为 ;当t ﹦ ,点P与点E重合;
(3)① 作点P关于直线EF的对称点P′.在运动过程中,若形成的四边形PEP′F为菱形,则t的值是多少?② 当t﹦2时,是否存在着点Q,使得△FEQ ∽△BEP ?若存在, 求出点Q的坐标;若不存在,请说明理由.
某巡警车在一条南北大道上巡逻,某天巡警车从岗亭A处出发,规定向北方向为正,当天行驶纪录如下(单位:千米)
+10,-9,+7,-15,+6,-5,+4,-2
(1)、最终巡警车是否回到岗亭A处?若没有,在岗亭何方,距岗亭多远?
(2)、巡警车行驶1千米耗油0.2升,油箱有油10升,够不够?若不够,途中还需补充多少升油?
如果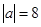 ,
,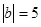 且
且 <0,
<0, <
< 求
求 的值
的值
先化简,再在数轴上表示下列各数,并用“<”号连接。
—(—3),0,-12 ,— ,
,
将下列各数填在相应的集合里。
—3.8,—10, 4.3,—∣—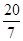 ∣, 42, 0,—(—
∣, 42, 0,—(—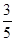 )
)
整数集合:{… };
分数集合:{… };
正数集合:{… };
负数集合:{… }。
(1)请用“>”、“<”、“=”填空:(3分)
①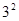 +
+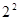 2×3×2
2×3×2
②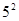 +
+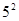 2×5×5
2×5×5
③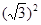 +
+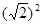 2×
2× ×
×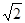
④ -6
-6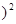 +
+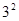 2×(-6)×3
2×(-6)×3
⑤ -
- +
+ -
- 2×(-2)×(-2)
2×(-2)×(-2)
(2)观察以上各式,请猜想 +
+ 与2ab的大小.
与2ab的大小.
(3)你能借助于完全平方公式证明你的猜想吗?试试看!