如图1,已知矩形纸片ABCD中,AB=6cm,若将该纸片沿着过点B的直线折叠(折痕为BM),点A恰好落在CD边的中点P处.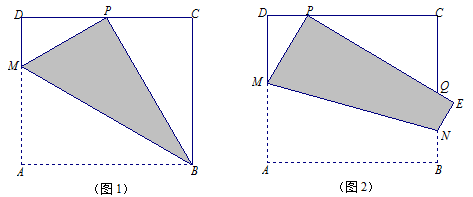
(1)求矩形ABCD的边AD的长.
(2)若P为CD边上的一个动点,折叠纸片,使得A与P重合,折痕为MN,其中M在边AD上,N在边BC上,如图2所示.设DP=x cm,DM=y cm,试求y与x的函数关系式,并指出自变量x的取值范围.
(3)①当折痕MN的端点N在AB上时,求当△PCN为等腰三角形时x的值;
②当折痕MN的端点M在CD上时,设折叠后重叠部分的面积为S,试求S与x之间的函数关系式
如图,已知AD∥BC,AB=AD+BC,E是CD的中点,求∠AEB的度数。 
如图,在△ABC中,E、F分别是AB、AC上的点。①AD平分∠BAC,②DE⊥AB,DF⊥AC,③AD⊥EF,以此三个中的两个为条件,另一个为结论,可构成三个命题,即:①②"③ ,①③"②,②③"① 。
。试判断上述三个命题是否正确(直接作答);
请证明你认为正确的命题。

如图,以△ABC两边AB、AC为边,向外作等边△ABD和等边△ACE,连接BE、CD交于O点.求证:△ADC≌△ABE
OA平分∠DOE
 |
如图,∠ABC=50°,AD垂直且平分BC于点D,∠ABC的平分线BE交AD于点E,连接EC,则∠AEC的度数是多少?
有特大城市A及两个小城市B、C,这三个城市共建一个污水处理厂,使得该厂到B、C两城市的距离相等,且使A市到处理厂的管线最短,试确定污水处理厂的位置。(保留作图痕迹)