一只不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有数字3、4、5、x.甲、乙两人每次同时从袋中各随机摸出1个球,并计算摸出的这2个小球上数字之和,记录后都将小球放回袋中搅匀,进行重复实验.实验数据如下表:
解答下列问题:
(1)如果实验继续进行下去,根据上表数据,出现“和为8”的频率将稳定在它的概率附近.估计出现“和为8”的概率是____________.
(2)如果摸出的这两个小球上数字之和为9的概率是 ,那么x的值可以取7吗?请用列表法或画树状图法说明理由;如果x的值不可以取7,请写出一个符合要求的x值.
,那么x的值可以取7吗?请用列表法或画树状图法说明理由;如果x的值不可以取7,请写出一个符合要求的x值.
已知:如图,AB是⊙O的直径,点C.D为圆上两点,且 ,CF⊥AB于点F,CE⊥AD的延长线于点E.
,CF⊥AB于点F,CE⊥AD的延长线于点E.

(1)试说明:DE=BF;
(2)若∠DAB=60°,AB=8,求△ACD的面积.
某校260名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.将各类的人数绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的,而条形图尚有一处错误.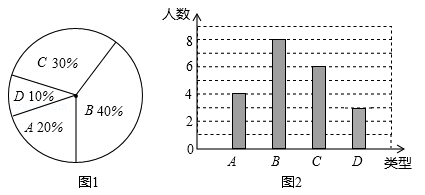
回答下列问题:
(1)写出条形图中存在的错误,并说明理由;
(2)写出这20名学生每人植树量的众数、中位数;
(3)在求这20名学生每人植树量的平均数时,小王是这样分析的:
① 小王的分析是从哪一步开始出现错误的?
② 请你帮他计算出正确的平均数,并估计这260名学生共植树多少棵.
作图:
在同一平面直角坐标系中有5个点:A(1,1),B(﹣3,﹣1),C(﹣3,1),D(﹣2,﹣2),E(0,﹣3).
(1)画出△ABC的外接圆⊙P,并指出点D与⊙P的位置关系;
(2)若直线l经过点D(﹣2,﹣2),E(0,﹣3),判断直线l与⊙P的位置关系.
如图1是立方体和长方体模型,立方体棱长和长方体底面各边长都为1,长方体侧棱长为2,现用60张长为6,宽为4的长方形卡纸,剪出这两种模型的表面展开图,有两种方法:
方法一:如图2,每张卡纸剪出3个立方体表面展开图;
方法二:如图3,每张卡纸剪出2个长方体表面展开图(图中只画出1个).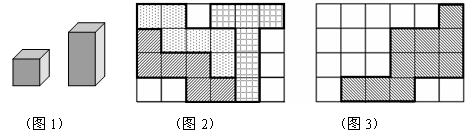
设用x张卡纸做立方体,其余卡纸做长方体,共做两种模型y个.要求制作的长方体的个数不超过立方体的个数.
(1)在图3中画出第二个长方体表面展开图,用阴影表示;
(2)请你写出y关于x的函数解析式,并注明自变量x的取值范围;
(3)设每只模型(包括立方体和长方体)平均获利为w(元),w满足函数 ,
,
若想将模型作为教具卖出获得最大利润,则应该制作立方体和长方体各多少个?最大利润是多少?