如图1是立方体和长方体模型，立方体棱长和长方体底面各边长都为1，长方体侧棱长为2，现用60张长为6，宽为4的长方形卡纸，剪出这两种模型的表面展开图，有两种方法：
方法一：如图2，每张卡纸剪出3个立方体表面展开图；
方法二：如图3，每张卡纸剪出2个长方体表面展开图（图中只画出1个）．
设用x张卡纸做立方体，其余卡纸做长方体，共做两种模型y个．要求制作的长方体的个数不超过立方体的个数．
（1）在图3中画出第二个长方体表面展开图，用阴影表示；
（2）请你写出y关于x的函数解析式，并注明自变量x的取值范围；
（3）设每只模型（包括立方体和长方体）平均获利为w（元），w满足函数
，
若想将模型作为教具卖出获得最大利润，则应该制作立方体和长方体各多少个？最大利润是多少？
在平面直角坐标系中，现将一块等腰直角三角形ABC放在第一象限，斜靠在两坐标轴上，且点A（0,2），点C（1,0），如图所示；抛物线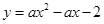
经过点B。
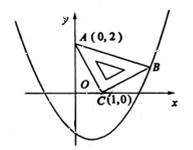
（1）求点B的坐标；
（2）求抛物线的解析式；
（3）在抛物线上是否还存在点P（点B除外），使ΔACP仍然是以AC为直角边的等腰直角三角形？若存在，求所以点P的坐标；若不存在，请说明理由。
某市种植某种绿色蔬菜，全部用来出口．为了扩大出口规模，该市决定对这种蔬菜的种植实行政府补贴，规定每种植一亩这种蔬菜一次性补贴菜农若干元．经调查，种植亩数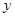
（亩）与补贴数额
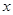（元）之间大致满足如图1所示的一次函数关系．随着补贴数额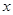的不断增大，出口量也不断增加，但每亩蔬菜的收益
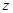（元）会相应降低，且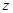与之间也大致满足如图2所示的一次函数关系．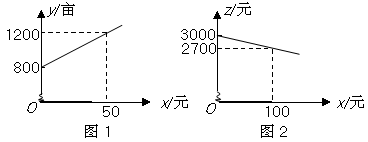
（1）在政府未出台补贴措施前，该市种植这种蔬菜的总收益额为多少？
（2）分别求出政府补贴政策实施后，种植亩数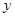和每亩蔬菜的收益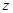与政府补贴数额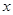之间的函数关系式；
（3）要使全市这种蔬菜的总收益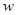
（元）最大，政府应将每亩补贴数额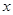定为多少？并求出总收益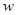的最大值．
如图，在Rt△ABC中，∠ACB=90°，AC=6㎝，BC=8㎝，P为BC的中点．动点Q从点P出发，沿射线PC方向以2㎝/s的速度运动，以P为圆心，PQ长为半径作圆．设点Q运动的时间为t s．
⑴当t=1.2时，判断直线AB与⊙P的位置关系，并说明理由；
⑵已知⊙O为△ABC的外接圆，若⊙P与⊙O相切，求t的值．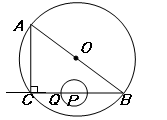
已知关于x的方程x2－2（k－1）x+ k2=0有两个实数根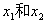
（1）求k的取值范围；
（2）若
，求k的值.
在一个不透明的盒子里，装有四个分别标有数字1，2，3，4的小球，它们的形状、大小、质地等完全相同.小明先从盒子里随机取出一个小球，记下数字为x；放回盒子摇匀后，再由小华随机取出一个小球，记下数字为y.
（1）用列表法或画树状图表示出（x，y）的所有可能出现的结果；
（2）求小明、小华各取一次小球所确定的点（x，y）落在反比例函数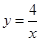
的图象上的概率；
（3）求小明、小华各取一次小球所确定的数x、y满足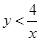
的概率.