(本小题满分10分)如图,在直角坐标系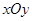 中,角
中,角 的顶点是原点,始边与
的顶点是原点,始边与 轴正半轴重合,终边交单位圆于点
轴正半轴重合,终边交单位圆于点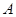 ,且
,且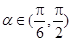 .将角
.将角 的终边按逆时针方向旋转
的终边按逆时针方向旋转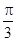 ,交单位圆于点
,交单位圆于点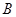 .记
.记 .
.
(1)若 ,求
,求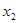 ;
;
(2)分别过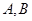 作
作 轴的垂线,垂足依次为
轴的垂线,垂足依次为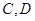 .记△
.记△ 的面积为
的面积为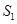 ,△
,△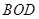 的面积为
的面积为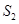 .若
.若 ,求角
,求角 的值.
的值.
若数列 满足
满足 ,则称数列
,则称数列 为“平方递推数列”.已知数列
为“平方递推数列”.已知数列 中,
中, ,点
,点 在函数
在函数 的图象上,其中
的图象上,其中 为正整数.
为正整数.
(1)证明数列 是“平方递推数列”,且数列
是“平方递推数列”,且数列 为等比数列;
为等比数列;
(2)设(1)中“平方递推数列”的前 项积为
项积为 ,即
,即 ,求
,求 ;
;
(3)在(2)的条件下,记 ,求数列
,求数列 的前
的前 项和
项和 ,并求使
,并求使 的
的 的最小值.
的最小值.
如图,公园要把一块边长为 的等边三角形
的等边三角形 的边角地修成草坪,
的边角地修成草坪, 把草坪分成面积相等的两部分,
把草坪分成面积相等的两部分, 在
在 上,
上, 在
在 上.
上.
(1)设 ,
, ,试用
,试用 表示函数
表示函数 ;
;
(2)如果 是灌溉水管,希望它最短,
是灌溉水管,希望它最短, 的位置应该在哪里?
的位置应该在哪里?
关于 的方程
的方程 的两根分别在区间
的两根分别在区间 与
与 内,求
内,求 的取值范围.
的取值范围.
解关于 的不等式
的不等式 .
.
已知正项数列 的前n项和为
的前n项和为 ,且
,且
(1)求 、
、 ;
;
(2)求证:数列 是等差数列;
是等差数列;
(3)令 ,问数列
,问数列 的前多少项的和最小?最小值是多少?
的前多少项的和最小?最小值是多少?