若数列 满足
满足 ,则称数列
,则称数列 为“平方递推数列”.已知数列
为“平方递推数列”.已知数列 中,
中, ,点
,点 在函数
在函数 的图象上,其中
的图象上,其中 为正整数.
为正整数.
(1)证明数列 是“平方递推数列”,且数列
是“平方递推数列”,且数列 为等比数列;
为等比数列;
(2)设(1)中“平方递推数列”的前 项积为
项积为 ,即
,即 ,求
,求 ;
;
(3)在(2)的条件下,记 ,求数列
,求数列 的前
的前 项和
项和 ,并求使
,并求使 的
的 的最小值.
的最小值.
(本小题满分12分)已知圆C: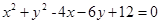 ,点A(3,5)求:
,点A(3,5)求:
(1)过点A的圆的切线方程;
(2)O是坐标原点,连接OA,OC,求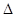 AOC的面积S.
AOC的面积S.
(本小题满分12分)某中学高二年级举行数学竞赛,共有800名学生参加.为了了解本次竞赛成绩,从中抽取了部分学生的成绩(得分均为整数,满分100分)进行统计。请你根据频率分布表,解答下列问题:
(1)填充下列频率分布表中的空格;
(2)估计众数、中位数和平均数;
(3)规定成绩不低于85分的同学能获奖,请估计在参加的800名学生中大概有多少名学生获奖?
| 分组(分数) |
频数 |
频率 |
| [60,70] |
① |
0.12 |
| [70,80] |
20 |
② |
| [80,90] |
③ |
0.24 |
| [90,100] |
④ |
⑤ |
| 合计 |
50 |
1 |
(本小题满分12分)一个盒子中装有5个编号依次为1、2、3、4、5的球,这5个球除号码外完全相同,有放回的连续抽取两次,每次任意地取出一个球.
(1)求事件A=“取出球的号码之和不小于6”的概率;
(2)设第一次取出的球号码为x,第二次取出的球号码为y,求事件B=“点(x,y)落在直线 y =" x+1" 上方”的概率.
(本小题满分10分)关于某设备的使用年限x和所支出的维修费用 (万元),有统计数据
(万元),有统计数据 ,由资料知
,由资料知 对
对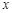 呈线性相关,并且统计的五组数据的平均值分别为
呈线性相关,并且统计的五组数据的平均值分别为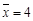 ,
, ,若用五组数据得到的线性回归方程
,若用五组数据得到的线性回归方程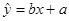 去估计,使用8年的维修费用比使用7年的维修费用多1.1万元.
去估计,使用8年的维修费用比使用7年的维修费用多1.1万元.
(1)求回归直线方程;
(2)估计使用年限为10年时,维修费用是多少?
过点A(8,6)引三条直线l1、l2、l3,它们的倾斜角之比为1∶2∶4,若直线l2的方程是y=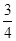 x,求直线l1、l3的方程
x,求直线l1、l3的方程