（本小题满分12分）贵阳六中织高二年级4个班的学生到益佰制药厂、贵阳钢厂、贵阳轮胎厂进行社会实践，规定每个班只能在这3个厂中任选择一个，假设每个班选择每个厂的概率是等可能的。（Ⅰ）求3个厂都有班级选择的概率；（Ⅱ）用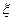
表示有班级选择的厂的个数，求随机变量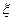的概率分布及数学期望
。
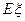(本小题满分12分)如图，在△ABC中，∠ABC=45°，∠BAC=90°，AD是BC上的高，沿AD把△ABD折起，使∠BDC=90°。
（1）证明：平面ＡＤＢ⊥平面ＢＤＣ；
（2）设BD=1，求三棱锥D—ＡＢＣ的表面积。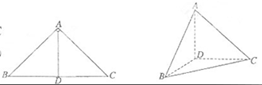
(本小题满分12分)已知圆C:
,直线
:mx－y＋1－m=0
(1)判断直线与圆C的位置关系。
（2）若直线与圆C交于不同两点A、B,且
=3
,求直线的方程。
(本小题满分12分)已知直三棱柱
中，
，
为
中点，
为
中点，侧面
为正方形。
(1)证明：
平面
；
(2)证明：
；
(本小题满分12分) 已知直线
经过直线
与直线
的交点
，且垂直于直线
.
（1）求直线的方程；
（2）求直线与两坐标轴围成的三角形的面积
.
（本小题满分16分）已知椭圆
：
的离心率为
，直线
：
与椭圆相切．
（1）求椭圆的方程；
（2）设椭圆的左焦点为
，右焦点为
，直线
过点且垂直与椭圆的长轴，动直线
垂直于直线于点
，线段
的垂直平分线交于点
，求点的轨迹
的方程.