(本小题满分12分)已知圆C: ,直线
,直线 :mx-y+1-m=0
:mx-y+1-m=0
(1)判断直线 与圆C的位置关系。
与圆C的位置关系。
(2)若直线 与圆C交于不同两点A、B,且
与圆C交于不同两点A、B,且 =3
=3 ,求直线
,求直线 的方程。
的方程。
已知椭圆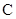 :
: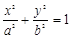 (
(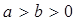 )的右焦点
)的右焦点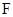 ,右顶点
,右顶点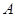 ,右准线
,右准线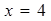 且
且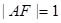 .
.
(1)求椭圆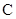 的标准方程;
的标准方程;
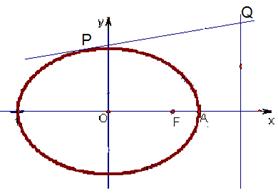
(2)动直线 :
: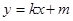 与椭圆
与椭圆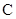 有且只有一个交点
有且只有一个交点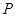 ,且与右准线相交于点
,且与右准线相交于点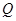 ,试探究在平面直角坐标系内是否存在点
,试探究在平面直角坐标系内是否存在点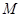 ,使得以
,使得以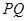 为直径的圆恒过定点
为直径的圆恒过定点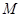 ?若存在,求出点
?若存在,求出点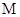 坐标;若不存在,说明理由.
坐标;若不存在,说明理由.
)已知某音响设备由五个部件组成,A电视机,B影碟机,C线路,D左声道和E右声道,其中每个部件工作的概率如图所示,能听到声音,当且仅当A与B中有一个工作,C工作,D与E中有一个工作;且若D和E同时工作则有立体声效果.
(1)求能听到立体声效果的概率;
(2)求听不到声音的概率.(结果精确到0.01)
设等差数列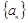 的前
的前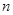 项和为
项和为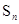 .且
.且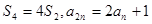 .
.
(1)求数列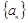 的通项公式;
的通项公式;
(2)若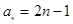 ,数列
,数列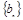 满足:
满足: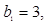
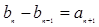
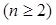 ,求数列
,求数列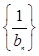 的前
的前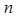 项和
项和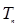 .
.
如图,在四棱锥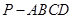 中,底面
中,底面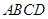 为菱形,
为菱形,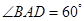 ,
,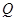 为
为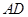 的中点.
的中点.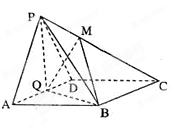
(1)若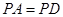 ,求证:平面
,求证:平面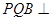 平面
平面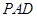 ;
;
(2)点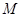 在线段
在线段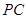 上,
上,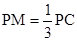 ,若平面
,若平面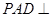 平面
平面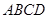 ,且
,且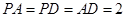 ,求二面角
,求二面角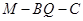 的大小.
的大小.
已知函数 .
.
(1)求 的最小正周期和最小值;
的最小正周期和最小值;
(2)若不等式 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.